Chứng minh OA=OA'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


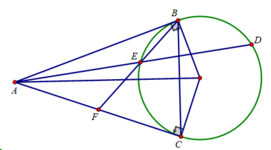
Có lẽ là đề nhầm (Đề này trong tuyển tập "Bộ đề hính học lớp 9). Đúng ra phải là BE cắt AC tại M

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là đường trung trực của BC
=>OA vuông góc với BC tạiH
=>OH*OA=OB^2; AH*AO=AB^2
b: Xét (O) có
ΔBFE nọi tiêp
BE là đường kính
DO đo: ΔBFE vuông tại F
Xét ΔBEA vuông tại B có BF là đường cao
nên AF*AE=AB^2
=>AH*AO=AF*AE
c: AH*AO=AF*AE
=>AH/AE=AF/AO
=>ΔAHF đồng dạngvới ΔAEO
=>góc AHF=góc AEO
=>góc AEO+góc OHF=180 độ

a) Do D thuộc đường tròn (O), AB là đường kính nên \(\widehat{BDC}=90^o\Rightarrow BD\perp AC\)
Xét tam giác vuông ABC, đường cao BD ta có:
\(AB^2=AD.AC\) (Hệ thức lượng)
b) Xét tam giác BEC có O là trung điểm BC; OH // CE nên OH là đường trung bình của tam giác. Vậy nên H là trung điểm BE.
Ta có OH // CE mà CE vuông góc AB nên \(OH\perp BE\)
Xét tam giác ABE có AH là trung tuyến đồng thời đường cao nên nó là tam giác cân.
Hay AB = AE.
Từ đó ta có \(\Delta ABO=\Delta AEO\left(c-c-c\right)\Rightarrow\widehat{OEA}=\widehat{OBA}=90^o\)
Vậy AE là tiếp tuyến của đường tròn (O)
c) Xét tam giác vuông OBA đường cao BH, ta có:
\(OB^2=OH.OA\) (Hệ thức lượng)
\(\Rightarrow OC^2=OH.OA\Rightarrow\frac{OH}{OC}=\frac{OC}{OA}\)
Vậy nên \(\Delta OHC\sim\Delta OCA\left(c-g-c\right)\Rightarrow\widehat{OHC}=\widehat{OCA}\)
d) Ta thấy \(\widehat{OCF}=\widehat{FCE}\left(=\widehat{OFC}\right)\)
Lại có \(\widehat{OCH}=\widehat{ACE}\left(=\widehat{OAC}\right)\)
Nên \(\widehat{HCF}=\widehat{FCA}\) hay CF là phân giác góc HCA.
Xét tam giác HCA, áp dụng tính chất đường phân giác trong tam giác, ta có:
\(\frac{HF}{FA}=\frac{HC}{CA}\Rightarrow FA.HC=HF.CA\left(đpcm\right)\)
ở phần c còn cạnh nào nữa để 2 tam giác đấy đồng dạng vậy cậu