Bài 8: cho hình thang vuông ABCD có góc A = góc D = 90o . AB = AD = 2cm, DC = 4cm. Tính hai góc còn lại của hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 5 2018
Đáp án cần chọn là: D
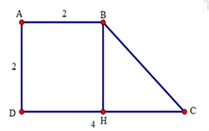
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .
PT
1
CM
13 tháng 10 2019
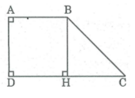
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠ A = ∠ D = 90 0 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ∆ BHC vuông cân tại H
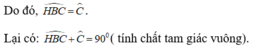
⇒ ∠ C = 45 0
∠ B + ∠ C = 180 0 (2 góc trong cùng phía bù nhau) ⇒ ∠ B = 180 0 – 45 0 = 135 0
NP
4
3 tháng 10 2021
Đáp án:
`hat{ABC} = 135^0`
`hat{C} = 45^0`
Giải thích các bước giải:
– Kẻ `OH ⊥ DC = {H}`
– Xét tứ giác `ABHD` có:
`AD = AB`
`hat{A} = hat{D} = 90^0`
`=> ABHD` là hình vuông
`=>` {DH=HC=2(cm)AD=BH=2(cm)
Xét `ΔBHC` vuông cân tại `H` có:
`hat {HBC} = hat{C} = 45^0`
`=> hat{ABC} = hat{HBC} + hat{ABH} = 45^0 + 90^0 = 135^0`
3 tháng 10 2021
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠∠A = ∠∠D = 900900 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: Δ∆BHC vuông cân tại H
⇒ ∠∠C = 450450
∠∠B + ∠∠C = 18001800 (2 góc trong cùng phía bù nhau) ⇒ ∠∠B = 18001800 – 450450 = 1350
HT
0
HN
0