Question

[a l i c e]

Cần dịch chuyển 1 cái hòm khối lượng m = 100kg đi 10m trên mặt phẳng ngang. Hệ số ma sát k = 0,1. Tính công tối thiểu cần thực hiện trong 2 trường hợp

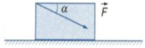
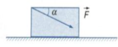
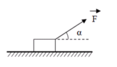
a) đẩy hòm theo phương làm với đường ngang 1 góc 30° và hướng xuống dưới

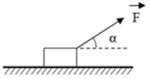
b) kéo hòm theo phương làm với đường ngang 1 góc 30° và hướng lên trên

Answer 1

[Nguyễn Việt Lâm]

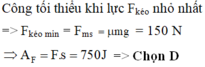
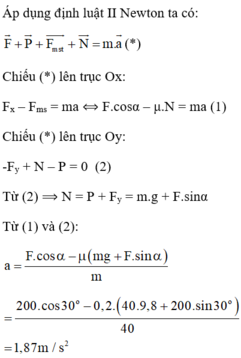
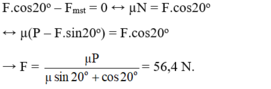
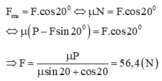
Đề vẫn không cho g, nên ta lấy \(g=10m/s^2\)

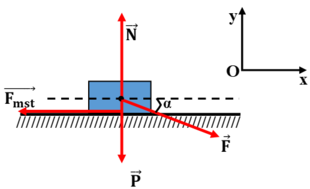
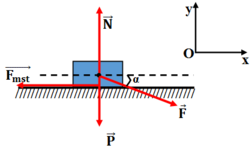
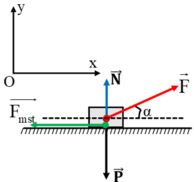
Hình vẽ cho trường hợp 1, các lực đều là vecto, trường hợp 2 tương tự:

Lực \(\overrightarrow{F}\) được phân tích thành 2 thành phần \(\overrightarrow{F_1}\) theo phương đứng hướng xuống và \(\overrightarrow{F_2}\) theo phương ngang

\(F_1=F.sin30^0\Rightarrow F_{ms}=\mu\left(P+F_1\right)=\mu\left(mg+\frac{F}{2}\right)\)

\(F_2=F.cos30^0=\frac{F\sqrt{3}}{2}\)

Vật chỉ dịch chuyển khi

\(F_2-F_{ms}\ge0\Leftrightarrow\frac{F\sqrt{3}}{2}-0,1\left(1000+\frac{F}{2}\right)\ge0\)

\(\Rightarrow F\ge\frac{200}{\sqrt{3}-1}=100\left(\sqrt{3}+1\right)\) (N)

Khi đó công tối thiểu cần thực hiện:

\(A=F_{min}.s.cos30^0=100\left(\sqrt{3}+1\right).10.\frac{\sqrt{3}}{2}=2366\left(J\right)\)

b/ Làm tương tự, chỉ là lần này lực \(F_1\) sẽ hướng lên, ngược chiều \(\overrightarrow{P}\)

\(F_1=F.sin30=\frac{F}{2}\Rightarrow F_{ms}=\mu\left(P-F_1\right)=\mu\left(mg-\frac{F}{2}\right)\)

\(F_2=F.cos30^0=\frac{F\sqrt{3}}{2}\)

Để vật dịch chuyển thì \(\frac{F\sqrt{3}}{2}-\mu\left(mg-\frac{F}{2}\right)\ge0\)

\(\Leftrightarrow F\ge\frac{200}{\sqrt{3}+1}=100\left(\sqrt{3}-1\right)\) (N)

Công tối thiểu cần thực hiện:

\(A=F_{min}.s.cos30^0=100\left(\sqrt{3}-1\right).10.cos30^0=664\left(J\right)\)