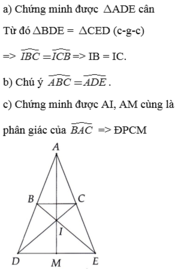
\(\Delta ABC\)cân ở A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD=CE. Gọi K là giao điểm của CD và BE. CMR:
a) BE=CD
b) \(\Delta BKD=\Delta CKE\)
c) AK là tia phân giác của \(\widehat{A}\)
d) Gọi M và N lần lượt là trung điểm của BC và DE. CMR: A,M,K,N thẳng hàng.