Chỉ mình câu c với ạ!!!
Plzzz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,A=\left(2x-7\right)^2=\left(2\cdot4-7\right)^2=1\\ B=\left(x-3\right)^3=\left(5-3\right)^3=8\\ C=\left(x^2-6x+9+x^2+6x+9\right):\left(x^2+9\right)\\ C=\left(2x^2+18\right):\left(x^2+9\right)=2\left(x^2+9\right):\left(x^2+9\right)\\ C=2\\ D=\left(5x-11-5x+9\right)^2=\left(-2\right)^2=4\)
a) \(A=4x^2-28x+49=\left(2x-7\right)^2=\left(2.4-7\right)^2=1^2=1\)
b) \(B=x^3-9x^2+27x-27=\left(x-3\right)^3\)
\(=\left(5-3\right)^3=2^3=8\)
c) \(C=\left[\left(x-3\right)^2+\left(x+3\right)^2\right]:\left(x^2+9\right)=\left(x^2-6x+9+x^2+6x+9\right):\left(x^2+9\right)=\left[2\left(x^2+9\right)\right]:\left(x^2+9\right)=2\)
d) \(D=\left(5x-11\right)^2-2\left(5x-11\right)\left(5x-9\right)+\left(5x-9\right)^2=\left(5x-11-5x+9\right)^2=\left(-2\right)^2=4\)
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

My classes usually learn at half past seven.


Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây

Câu 1:
\(C=\dfrac{2}{1.4}+\dfrac{2}{4.7}+\dfrac{2}{7.10}+...+\dfrac{2}{97.100}\)
\(C=\dfrac{2}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{97.100}\right)\)
\(C=\dfrac{2}{3}.\left(\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(C=\dfrac{2}{3}.\left(\dfrac{1}{1}-\dfrac{1}{100}\right)\)
\(C=\dfrac{2}{3}.\dfrac{99}{100}\)
\(C=\dfrac{33}{50}\)
Câu 3:
a) Gọi ƯCLN(2n+5;n+3)=d
\(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\n+3⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\2.\left(n+3\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+6⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+6\right)-\left(2n+5\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{2n+5}{n+3}\) là p/s tối giản
b) Để \(B=\dfrac{2n+5}{n+3}\) là số nguyên thì \(2n+5⋮n+3\)
\(2n+5⋮n+3\)
\(\Rightarrow2n+6-1⋮n+3\)
\(\Rightarrow1⋮n+3\)
\(\Rightarrow n+3\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng giá trị:
\(n+3=-1\rightarrow n=-4\)
\(n+3=1\rightarrow n=-2\)
Vậy \(n\in\left\{-4;-2\right\}\)
 giúp mình với plzzz , chiều mình nộp r ạ
giúp mình với plzzz , chiều mình nộp r ạ 
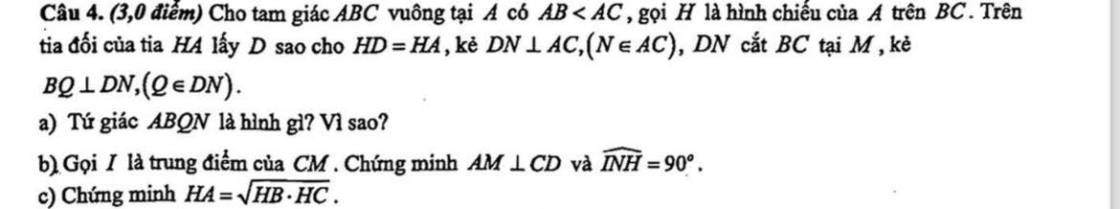
 chỉ mình câu này với ạ
chỉ mình câu này với ạ


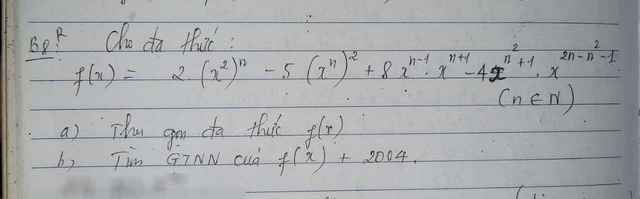
Nói tới những người nông dân,người nghèo khổ,..thời phong kiến