Xin giúp em câu 5 ạ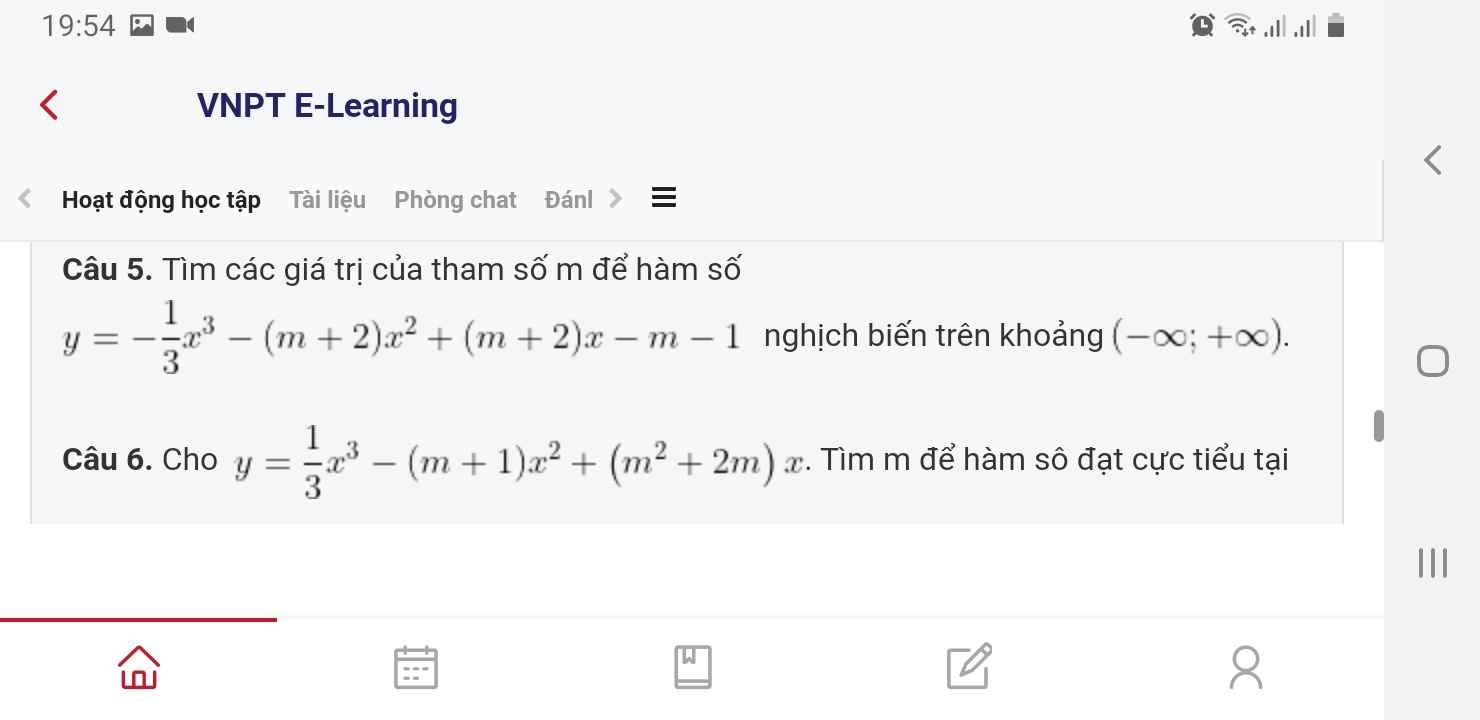
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vận tốc của chất điểm:
\(v\left(t\right)=s'\left(t\right)=3t^2-6t+9=3\left(t-1\right)^2+6\ge6\)
Dấu "=" xảy ra khi \(t-1=0\Rightarrow t=1s\)
Dạ em cảm ơn rất nhiều ạ, nhưng nếu được thầy có thể giải thích giúp em làm sao ra đc :S'(t) ạ ?


\(4,\\ b,B=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\ge3\sqrt[3]{\dfrac{xyz}{xyz}}=3\)
Dấu \("="\Leftrightarrow x=y=z\)
\(c,x+y=4\Leftrightarrow x=4-y\\ \Leftrightarrow C=\left(4-y\right)^2+y^2\\ C=16-8y+y^2+y^2=2\left(y^2-4y+4\right)+8\\ C=2\left(y-2\right)^2+8\ge8\\ C_{min}=8\Leftrightarrow x=y=2\)

a, cường độ dđ mạch
\(I=\dfrac{U}{R_{td}}=\dfrac{12}{10+5}=0,8\left(A\right)\)
\(\Rightarrow U_1=I.R_1=8\left(V\right)\)
\(\Rightarrow U_2=I.R_2=5.0,8=4\left(V\right)\)
b, \(\Rightarrow U_1=\dfrac{4}{2}=2\left(V\right)\)
\(I=I_2=\dfrac{4}{5}=0,8\left(A\right)\)
\(I_1=\dfrac{2}{10}=0,2\left(A\right)\)
\(I_3=I_2-I_1=0,6\left(A\right)\)
\(\Rightarrow R_3=\dfrac{U_1}{I_3}=\dfrac{2}{0,6}=\dfrac{10}{3}\left(\Omega\right)\)

Có: `-C_2021 ^0 +C_2021 ^1 -C_2021 ^2 +....+C_2021 ^2019-C_2021 ^2020 -C_2021 ^2021 =-1-1=-2`
Mà `C_2021 ^0 +C_2021 ^1 +C_2021 ^2 +....+C_2021 ^2019 +C_2021 ^2020 +C_2021 ^2021 =2^2021`
`=>2(C_2021 ^1 + C_2021 ^3 +C_2021 ^5 +...+C_2021 ^2017 + C_2021 ^2019 )=-2+2^2021`
`=>C_2021 ^1 + C_2021 ^3 +...+C_2021 ^2017 + C_2021 ^2019 =-1+2^2020`





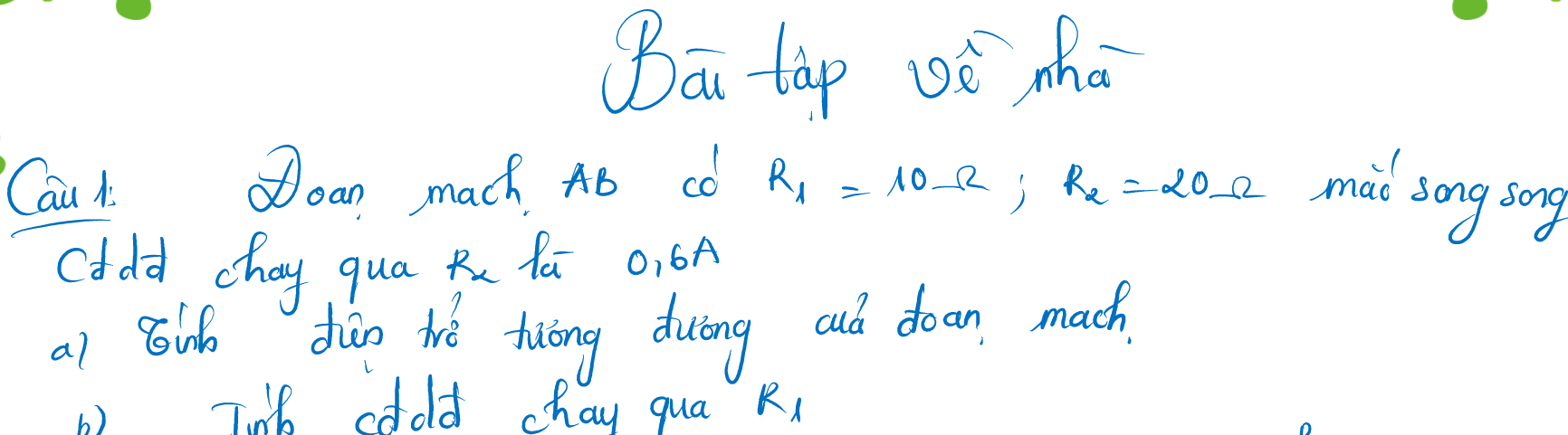
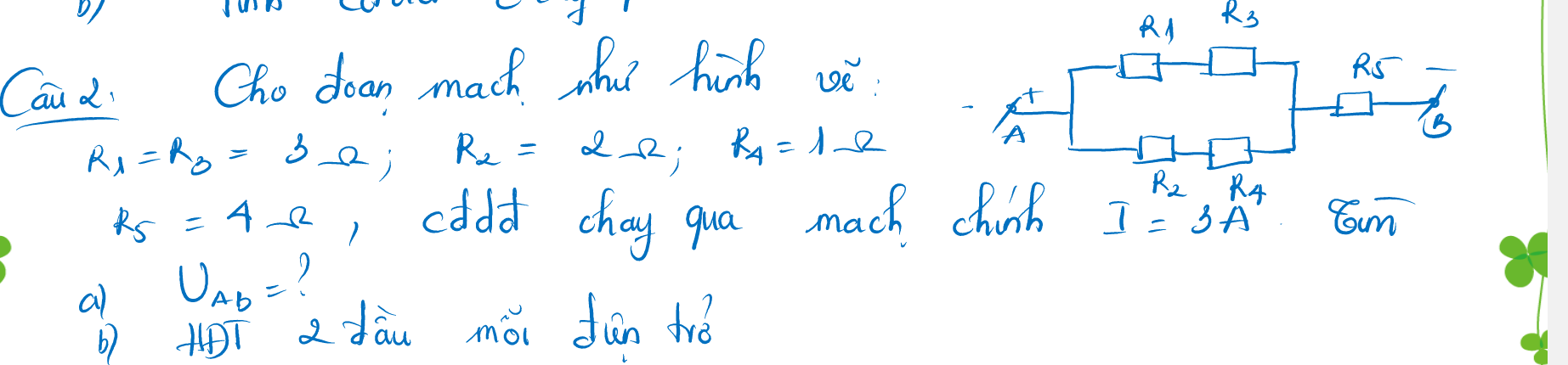


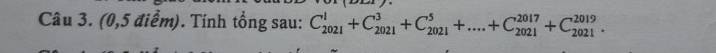


\(y'=-x^2-2\left(m+2\right)x+m+2\)
Hàm nghịch biến trên R khi và chỉ khi:
\(-x^2-2\left(m+2\right)x+m+2\le0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+2\right)^2+m+2\le0\)
\(\Leftrightarrow\left(m+2\right)\left(m+3\right)\le0\)
\(\Rightarrow-2\le m\le-3\)