tìm các số nguyên a và b biết b.a=16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1 tháng 1 2016
ai ra kết quả nhanh nhất hoạc có bài làm đúng nhất mình cho 2 **** ( mình có 4 nick phụ luôn )
26 tháng 12 2017
a ) 15 + ( -16 ) + a = -10
-1 + a = -10
a = -10 - ( -1 )
a = -9
b ) a + ( -11 ) + ( -25 ) = 0
a + ( -36 ) = 0
a = 0 - ( -36 )
a = 36
12 tháng 4 2022
a, Gọi \(n_B=a\left(mol\right)\rightarrow n_A=3a\left(mol\right)\)
Theo đề bài: \(a+3a=\dfrac{2,4.10^{23}}{6.10^{23}}=0,4\left(mol\right)\)
\(\Leftrightarrow a=0,1\left(mol\right)\)
b, Gọi \(M_B=b\left(\dfrac{g}{mol}\right)\rightarrow M_A=0,375b\left(\dfrac{g}{mol}\right)\)
Theo đề bài: \(0,1b+0,3.0,375b=13,6\)
\(\Leftrightarrow b=64\left(\dfrac{g}{mol}\right)\\ \rightarrow\left\{{}\begin{matrix}M_B=64\left(\dfrac{g}{mol}\right)\\M_A=\dfrac{3}{8}.64=24\left(\dfrac{g}{mol}\right)\end{matrix}\right.\)
=> A và B lần lượt là Cu và Mg
c, \(\left\{{}\begin{matrix}n_{Cu}=\dfrac{6,8}{13,6}.0,3=0,15\left(mol\right)\\n_{Mg}=\dfrac{0,15}{3}=0,05\left(mol\right)\end{matrix}\right.\)
PTHH: Cu + Cl2 --to--> CuCl2
0,15 -> 0,15
Mg + Cl2 --to--> MgCl2
0,05 -> 0,05
\(V_{Cl_2}=\left(0,05+0,15\right).22,4=4,48\left(l\right)\)
8 tháng 1 2017
\(\frac{ab+ac}{2}=\frac{bc+ab}{3}=\frac{ca+bc}{4}\)
( ta lần lược lấy - (1) + (2) + (3) = (1) - (2) + (3) = (1) + (2) - (3) được)
\(=\frac{2bc}{5}=\frac{2ca}{3}=\frac{2ab}{1}\)
Ta thấy rằng a,b,c không thể = 0 vì như vậy thì a + b + c \(\ne69\)
\(\Rightarrow\hept{\begin{cases}a=\frac{c}{5}\\b=\frac{c}{3}\end{cases}}\)
Thế vào: a + b + c = 69
\(\Leftrightarrow\frac{c}{5}+\frac{c}{3}+c=69\)
\(\Rightarrow c=45\)
\(\Rightarrow\hept{\begin{cases}a=9\\b=15\end{cases}}\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
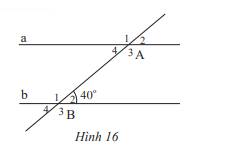
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)