Giúp ik mà, 9h15 nộppppp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 3 + 32 + 33 + 34 + .....+3100
3.A = 32 + 33 + 34 +......+ 3100 + 3101
3A - A = 3101 - 3
2A = 3101 - 3
2A + 3 = 3101 - 3 + 3
2A + 3 = 3101
2A + 3 = 34n+1 \(\Leftrightarrow\) 3101 = 34n+1 \(\Leftrightarrow\) 101 = 4n + 1 \(\Leftrightarrow\) 4n = 100 \(\Leftrightarrow\) n = 25
Kết luận n = 25 là giá trị thỏa mãn đề bài

a: Xét ΔAHD có
AP là đường cao ứng với cạnh HD
AP là đường trung tuyến ứng với cạnh HD
Do đó: ΔAHD cân tại A
mà AP là đường cao ứng với cạnh HD
nên AP là đường phân giác ứng với cạnh HD
Xét ΔAHE có
AQ là đường cao ứng với cạnh HE
AQ là đường trung tuyến ứng với cạnh HE
Do đó: ΔHAE cân tại A
mà AQ là đường cao ứng với cạnh HE
nên AQ là đường phân giác ứng với cạnh HE
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của DE
a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)
góc APD = APH=90o
AD = AH
AP chung
=> AD=AH (1)
CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)
=> AE= AH (2)
Từ 1 và 2 => AD= AE
=> A là trung điểm của DE
b) Xét \(\Delta DHE\) có:
DP=PH; HQ=QE
=> PQ là đg trung bình của tam giắc DHE
=> PQ// DE; PQ=1/2 DE
c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o
=> Tứ giác APHQ là HCN
=> PQ=AH ( theo t/c HCN)

A B A' B'
Ta vẽ ảnh A'B' bằng AB
Vẽ A'B' bằng nét đứt
Vẽ khoảng cách từ AB đến gương bằng khoảng cách từ gương đến A'B'
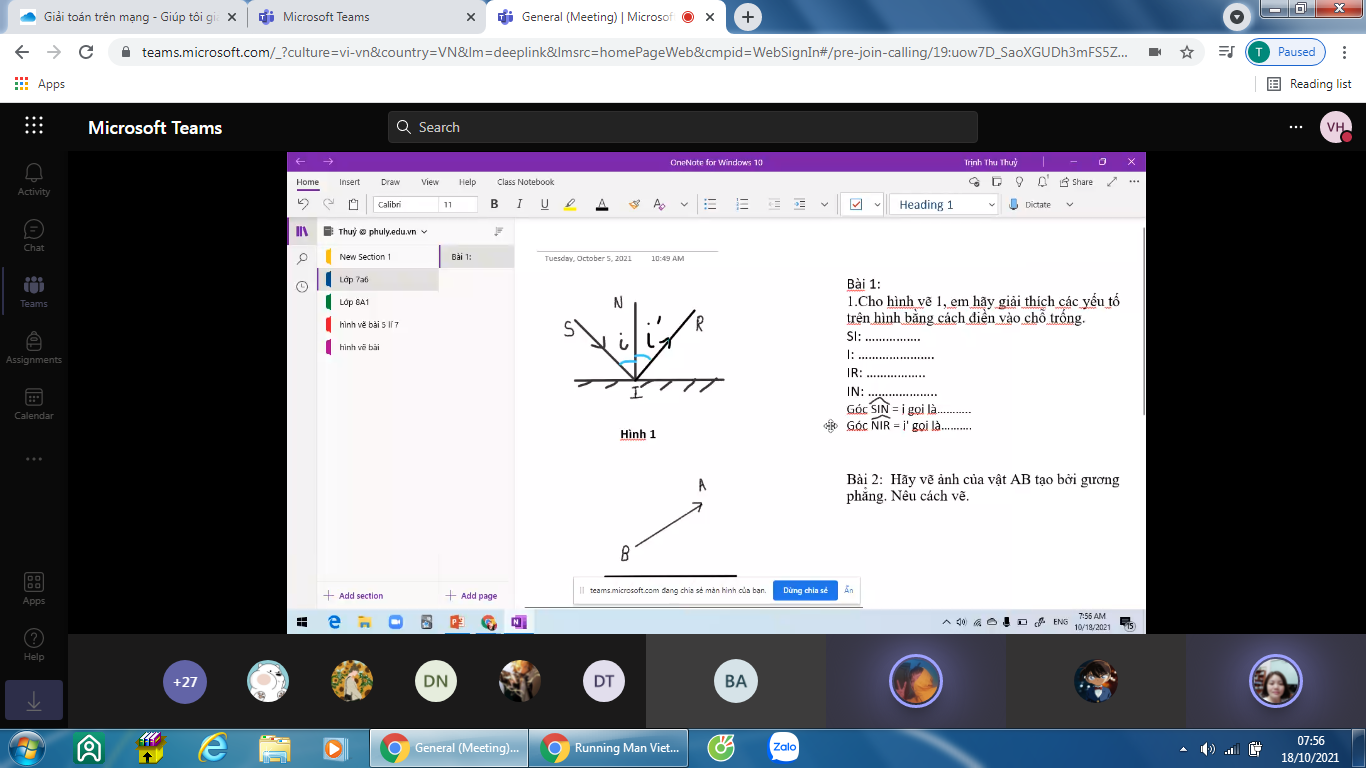
Bài 1. SI: tia tới
I: điểm tới
IR: TIA PHẢN XẠ
IN: tia pháp tuyến
\(i\): góc tới
\(i'\): góc phản xạ

a: Chiều dài là 60*5/8=7,5*5=37,5(m)
Chiều rộng là 60-37,5=22,5(m)
Diện tích là 37,5*22,5=843,75m2
b: Gọi diện tích trồng cây ăn quả và diện tích trồng hoa lần lượt là x,y
Theo đề, ta có: x+y=843,75 và 1/2x=2/5y
=>x=375 và y=468,75



Bài 5:
a: \(x^2+y^2-2x+4y-20=0\)
=>x^2-2x+1+y^2+4y+4=25
=>(x-1)^2+(y+2)^2=25
Khi x=4 và y=2 thì ta có: (4-1)^2+(2+2)^2=3^2+4^2=25
=>M thuộc (C)
b: Tâm là I(1;-2); R=5; M(4;2)
vecto IM=(3;4)
=>(d) có VTPT là (3;4)
Phương trình tiếp tuyến tại M của (C) là:
3(x-4)+4(y-2)=0
=>3x+4y-20=0
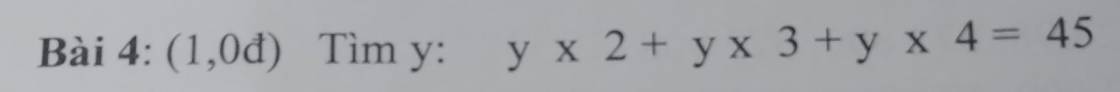 giúp tui ik mà
giúp tui ik mà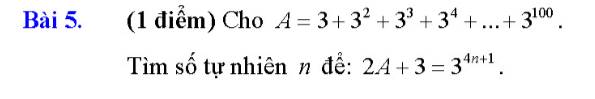 giúp tui ik mà
giúp tui ik mà


 giúp mik ik mà mik cần gấp lắm
giúp mik ik mà mik cần gấp lắm