Cho ΔABC và ΔA'B'C', biết AB=8cm, AC=6cm, BC=10cm. Cạnh lớn nhất của ΔA'B'C' là 25cm. Tính cạnh nhỏ nhất của ΔA'B'C'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 2 2022
e làm a,b chung luôn nha chị
Xét tam giác ABC và tam giác A`B`C`, có:
\(\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( gt )
Góc A = góc A` = 90 độ
=> tam giác ABC đồng dạng tam giác A`B`C`
=>\(\dfrac{AC}{A`C`}=\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( tính chất 2 tam giác đồng dạng )
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)
26 tháng 3 2022
a: \(AC=\sqrt{BC^2-AB^2}=5\sqrt{3}\left(cm\right)\)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
=>BD là đường trung trực của AE
hay BD\(\perp\)AE
CM
19 tháng 8 2017
ΔA'B'C'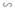 
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒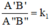 
ΔA''B''C''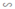 
ΔABC theo tỉ số đồng dạng k2 ⇒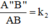 
Mà ΔA'B'C'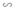 
ΔA''B''C''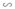; ΔA''B''C'' 
ΔABC
⇒ ΔA'B'C'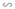 
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
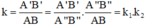
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
Mệnh đề B đúng
Hình chữ nhật có 2 trục đối xứng (là 2 đường thẳng đi qua trung điểm của các cạnh đối diện)