Cho tam giác ABC vuông tại A.Vẽ AH vuông góc Bc.Vẽ các tia Ax và Ay sao cho AB,AC lần lượt là các tia phân giác của các góc HAx và Hay.Vẽ BD vuông góc Ax; CE vuuong góc Ay
a) Tính số đo của góc xAy
b) CM: BD+CE=BC
c) CM: tam giác HDE vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2017
1) Ta có: ^BAC+^BAD=^BAC+^CAE=^BAC=900 => ^DAC=^BAE
Xét \(\Delta\)DAC & \(\Delta\)BAE: AD=AB; ^DAC=^BAE; AC=AE => \(\Delta\)DAC=\(\Delta\)BAE (c.g.c)
=> CD=BE (2 cạnh tương ứng)
Gọi CD giao BE tại P, AB giao CD tại Q
Do \(\Delta\)DAC=\(\Delta\)BAE (cmt) => ^D1=^B1 (2 góc tương ứng)
Xét 2 tam giác: \(\Delta\)DAQ và \(\Delta\)BPQ: ^DQA=^BQP (đối đỉnh), ^D1=^B1
=> ^DAQ=^BPQ => ^BPQ=900 hay CD vuông góc với BE.
2) Trên tia đối của AM lấy điểm F sao cho AF=2AM.
Chứng minh được: \(\Delta\)ABM=\(\Delta\)FCM (c.g.c) => AB=FC. Mà AB=AD => FC=AD
=> ^ABM=^FCM (2 góc tương ứng). Mà 2 góc này so le trong => AB//FC
=> ^BAC+^ACF=1800. (1)
Lại có: ^BAC+^BAD+^CAE+^EAD=3600 => ^EAD+^BAC=3600-^BAD-^CAE=1800 (2)
Từ (1) và (2) => ^ACF=^EAD.
Xét \(\Delta\)ACF & \(\Delta\)EAD: AC=EA; ^ACF=^EAD; CF=AD => \(\Delta\)ACF=\(\Delta\)EAD (c.g.c)
=> AF=DE (2 cạnh tương ứng). Thấy AF=2AM => DE=2AM.
3) Gọi AM cắt DE tại K
Ta có: \(\Delta\)ACF=\(\Delta\)EAD (cmt) => ^A1=^E1.
Mà ^A1+^EAK=900 => ^E1+^EAK=900 => \(\Delta\)EKA vuông tại K hay AM vuông góc với DE.
4) Có: ^ACH+^HAC=900. Mà ^OAE+^HAC=900 => ^ACH=^OAE hay ^ACM=^OAE.
Xét \(\Delta\)AMC & \(\Delta\)EOA có: AC=AE, ^A1=^E1; ^ACM=^OAE => \(\Delta\)AMC=\(\Delta\)EOA (g.c.g)
=> AM=EO (2 cạnh tương ứng).
Lại có: DE=2AM (cmt) => DE=2EO (O\(\in\)DE) hay là trung điểm của DE (đpcm).
CM
17 tháng 2 2018
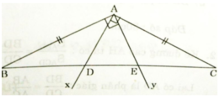
Ta có: Ax ⊥ AC (gt)
⇒ ∠DAC = 90o
⇒ ∠BAD = 135o - 90o = 45o
Tương tự ta có :
∠CAE = ∠BAD = 45o
Do đó AE và AB là phân giác trong và ngoài của góc ∠DAC
Ta có :
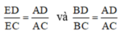
Xét ΔBAD và ΔCAE có:
∠BAD = ∠CAE ( = 45o )
AB = AC ( Δ ABC cân tại A)
∠ABD = ∠ACE (Δ ABC cân tại A)
⇒ ΔBAD = ΔCAE (g.c.g)
⇒ BD = EC
Thay vào (1) ta có : BD2 = BC.DE (đpcm).
8 tháng 1 2022
a: Xét ΔACB cân tại A có AH là đường cao
nên AH là đường phân giác
b: Xét ΔAEH vuông tại E và ΔAFH vuông tại F có
AH chung
\(\widehat{HAE}=\widehat{HAF}\)
Do đó: ΔAEH=ΔAFH
Suy ra: AE=AF