ho ∆ABC có M và N lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia NM lấy điểm D sao cho NM = ND. Gọi I là trung điểm của đoạn thẳng AM. a) Tứ giác ADCM là hình gì? Vì sao? b) Chứng minh B, I, D thẳng hàng. c) Qua điểm D kẻ đường thẳng song song với AC, cắt đường thẳng BC tại E. Đường thẳng IN cắt DE tại F. Tìm điều kiện của ∆ABC để tứ giác MNFE là hình thang cân.
mn giúp mk với

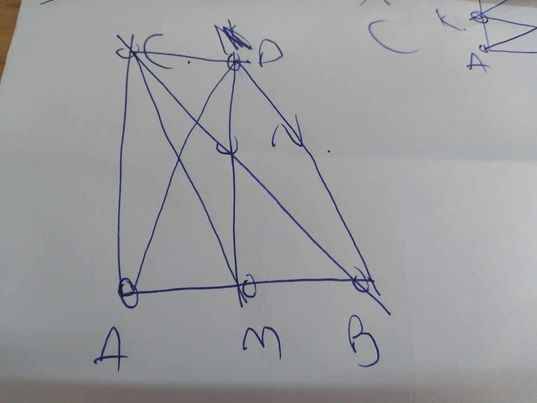


a: Xét tứ giác AMCD có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo MD
Do đó: AMCD là hình bình hành
b: Ta có: AMCD là hình bình hành
nên AD//MC và AD=MC
hay AD//MB và AD=MB(Vì MB=MC)
Xét tứ giác ABMD có
AD//MB
AD=MB
Do đó: ABMD là hình bình hành
Suy ra: Hai đường chéo AM và BD cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của AM
nên I là trung điểm của BD
hay B,I,D thẳng hàng