với a thuộc z so sánh a^2 và 2a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Có 3 trường hợp:
1) a2 > 2a (VD: 32 > 2.3)
2) a2 < 2a (VD:12 < 2.1)
3) a2 = 2a (VD:02 = 2.0)

Có đủ 3 trường hợp:
+) a2 = 2a khi a = 0 hoặc 2
Giải cụ thể:
a2 = 2a => a2 - 2a = 0
=> a(a-2) = 0 => a = 0;2
+) a2 > 2a khi a > 2 hoặc a < 0
+) a2 < 2a khi 0 < a < 2

a) ĐKXĐ: \(x\ge0,x\ne9\)
\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)
b) \(A=\dfrac{3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{64}+3}=\dfrac{3}{8+3}=\dfrac{3}{11}\)
c) \(2A=\dfrac{6}{\sqrt{x}+3}=1\Rightarrow\sqrt{x}+3=6\Rightarrow x=9\left(tm\right)\)
g) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
h) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
k) \(2A=\dfrac{6}{\sqrt{x}+3}=m\)

với \(a\in Z\)
Xét 3 trường hợp
Khi a< 0 thì a2 > 2a ( 1 )
Khi a = 0, 1 , 1 thì a2 = 2a ( 2 )
Khi a> 2 thì a2 > 2a ( 3 )
Từ ( 1) , ( 2 ) , ( 3 ) \(\Rightarrow a^2\ge2a\)

câu 1
nếu a>0 thì (-7).a >(-10).a
nếu a=0 thì 2 cái bằng nhau vì cùng bằng 0
câu 2
nếu a<3 suy ra a-3 sẽ ra số âm thì 15.(a-3)<11.(3-a)
nếu a bằng 3 thì bằng nhau vì a-3=0
Với \(a\in Z\)và \(a\ge0\)ta có :
\(\left(-7\right)>\left(-10\right)\)
\(\Rightarrow\left(-7\right)a>\left(-10\right)a\)
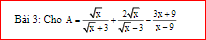
TH1: a Là số âm ta có:
\(a^2\ge0\)với mọi a
\(2a< 0\)với mọi a
\(\Rightarrow a^2>2a\)
TH2: \(a=1\)
\(\Rightarrow a^2< 2a\left(1< 2\right)\)
TH3:\(a=0;a=2\)
\(\Rightarrow a^2=2a\left(4=4hoặc0=0\right)\)
TH4:\(a\ge3\)
\(\Rightarrow a^2>2a\)
VẬY:\(a^2>2a\)Khi \(a< 0;a\ge3\)
\(a^2=2a\)Khi \(a=0;a=2\)
\(a^2< 2a\)Khi \(a=1\)