Cho góc bẹt xOy trên tia Ox lấy điểm B sao cho OB =5cm gọi M là trung điểm của OB Trên tia Oy lấy điểm N sao cho ON=OM
a, Tính độ dài đoạn thẳng BN \BN=7,5
b,trên một nữa mặt phẳng có bờ là đường thẳng xy Vẽ tia Oz sao cho xOz =80 độ tính zOy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác OMA và tam giác OMB:
OM chung.
OA = OB (gt).
MA = MB (M là trung điểm của đoạn thẳng AB).
=> ∆ OMA = ∆ OMB (c - c - c).
b) Xét tam giác OAB:
OA = OB (gt).
=> Tam giác OAB cân tại O.
Mà OM là đường trung tuyến (M là trung điểm của đoạn thẳng AB).
=> OM là đường cao (Tính chất tam giác cân).
=> OM vuông góc với AB.
c) Xét tam giác HON vuông tại H và tam giác KON vuông tại K:
ON chung.
\(\widehat{HON}=\widehat{KON}\) (∆ OMA = ∆ OMB).
=> Tam giác HON = Tam giác KON (cạnh huyền - góc nhọn).
=> NH = NK (2 cạnh tương ứng).
d) Xét tam giác OHK:
OH = OK (Tam giác HON = Tam giác KON).
=> Tam giác OHK cân tại O.
Xét tam giác OHK cân tại O:
OP là trung tuyến (P là trung điểm của đoạn HK).
=> OP là phân giác góc O (Tính chất tam giác cân). (1)
Xét tam giác OAB cân tại O:
OM là trung tuyến (M là trung điểm của đoạn AB).
=> OM là phân giác góc O (Tính chất tam giác cân). (2).
=> Ba điểm O, M, P thẳng hàng.

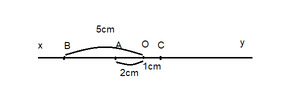
a. ta có :
OB - OA = AB
Hay 5 - 2 = AB
5 - 2 =3(cm) vậy AB= 3cm
ta có :
OB + OC = BC
Hay 5 + 1 = BC
5 + 1 = 6 (cm) vậy BC = 6 cm
b, nếu A là trung điểm BC thì : \(AB=AC=\dfrac{BC}{2}=\dfrac{6}{2}=3cm\left(\text{đ}pcm\right)\)
c,
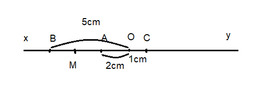
M là trung điểm AB thì : \(BM=AM=\dfrac{AB}{2}\)
AM là : \(\dfrac{AB}{2}=\dfrac{3}{2}=1,5\left(cm\right)\)
ta có : OA+AM=OM
Hay 2+1,5=OM
2+1,5=3,5(cm) vậy OM = 3,5 cm
tại mik vễ trên máy tính nên k được chuẩn cho lắm , cậu thông cảm nha