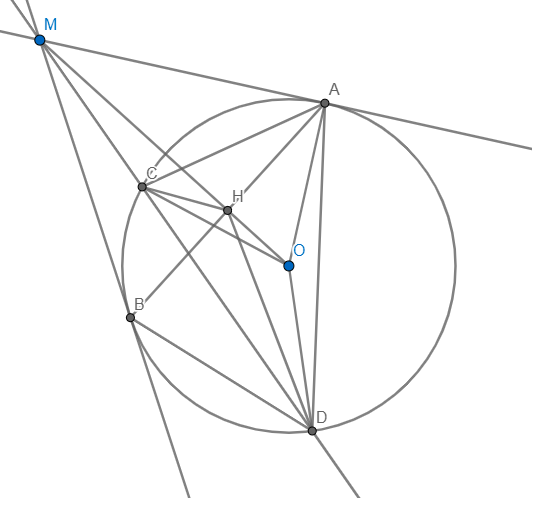
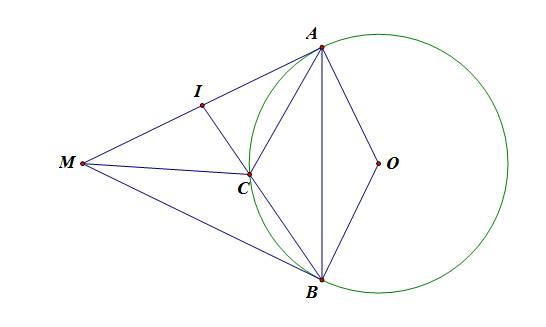
Từ M ở ngoài (O,r) Vẽ 2 tiếp tuyến MA và MB (A;B là tiếp điểm ) và đường thẳng đi qua M cắt đường tròn tại C và D. Gọi I là trung điểm CD, gọi E; F và K lần lượt là các giao điểm đường thẳng AB với đường thẳng MO;MD;OI
Chứng minh
a) r^2=OE.OM=OI.OA
b) M;A;B;O;I cùng thuộc 1 đường tròn