Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh AC. Kẻ AM vuông góc BD. CM: góc MCH = góc HDM.
Cần gấp!! Ai lm nhanh và đúng tick 3 tick!!
Thanks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
3 tháng 7 2018
a) Xét tam giác ABD và tam giác HBD ta có :
BD là cạnh chung
góc ABD = góc HBD ( vì BD là tia phải giác )
góc BAD = góc BHD = 90o
Do đó tam giác ABD = tam giác HBD ( cạnh huyền - góc nhọn )
Gọi G là điểm cắt giữa đoạn thẳng AH và BD
Vì tam giác ABD = tam giác HBD => AB=BH ( 2 cạnh tương ứng )
Xét tam giác ABG và tam giác BHG có :
AB = BH
góc ABG = góc HBG ( vì B là góc phân giác )
BG chung
Do đó tam giác AGB = tam giác BGH (c-g-c)
=> góc AGB = góc HGB ( 2 góc tương ứng )
b) Từ a => AB = BH ( 2 cạnh tương ứng )
Xét tam giác ABC và tam giác HBK có :
AB = BH
góc B chung
góc BAC = góc BHK = 90o
Do đó tam giác ABC = tam giác HBK ( cạnh góc vuông - góc nhọn )
23 tháng 12 2019
a ) Xét \(\Delta\)ABD và \(\Delta\)EBD có :
- BD : cạnh chung
- BÂD = BÊD ( = 90° )
- Góc ABD = Góc EBD ( vì BD là phân giác của góc ABE )
\(\Rightarrow\)\(\Delta\)ABD = \(\Delta\)EBD ( cạnh huyền - góc nhọn )
b ) Xét \(\Delta\) ADF và\(\Delta\)EDC có :
- AD = DE ( \(\Delta\)BDA = \(\Delta\)BDE )
- Góc ADF = Góc EDC ( đối đỉnh )
- DÂF = DÊC ( = 90° )
\(\Rightarrow\)\(\Delta\)ADF = \(\Delta\)EDC ( cạnh góc vuông - góc nhọn kề )
\(\Rightarrow\)FD = CD ( 2 cạnh tương ứng )
23 tháng 4 2023
`@` `\text {dnammv}`
`a,`
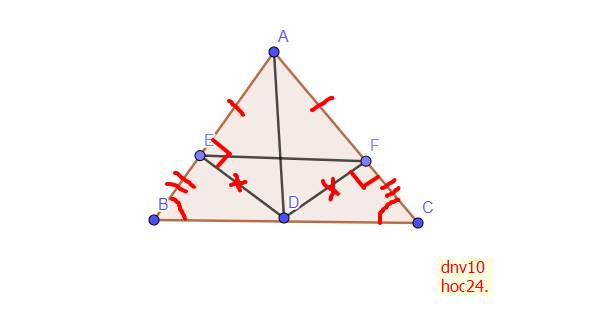
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`
H ở đâu ra vậy bạn??
À quên còn đường cao AH nữa >.< sr nhé giải đc giải hộ mk nha