Cho tam giác ABC nội tiếp (O) có đường kính AB ( AC< BC). Trên dây BC lấy điểm \(H\ne B\)và \(H\ne C\). AH cắt (O) tại D. Kẻ HQ vuông góc AB (\(Q\in AB\)) Đường thẳng CQ cắt (O) tại F.
a, CMR tứ giác ACHQ là tứ giác nội tiếp.
b, Gọi M,N lần lượt là hình chiếu của F trên AC và BC. CMR MN, AB ,DF đồng quy.

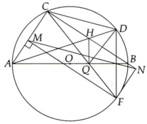
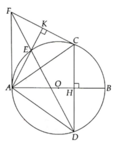
b/ Gọi G là giao điểm của AB và DF
Ta có :
Góc ACQ = góc AHQ ( t/g ACHQ n.t )
Góc ACQ = góc ADF ( 2 góc n.t chắn cung AF )
=> Góc AHQ = góc ADF
Mà 2 góc ở vị trí đồng vị
Nên \(HQ//DF\)
Mặc khác \(HQ\perp AB\)tại Q
=> \(DF\perp AB\)tại G
Xét tứ giác GBNF ta có:\(B\widehat{G}F+B\widehat{N}F=180^0\)
=> Tứ giác GBNF nội tiếp =>\(N\widehat{G}F=N\widehat{B}F\)
Mà \(N\widehat{B}F=C\widehat{A}F\)( tứ giác ACBF n.t (O))
Nên \(N\widehat{G}F=C\widehat{A}F\left(1\right)\)
Xét tứ giác GMAF ta có: \(A\widehat{M}F=A\widehat{G}F\left(=90^0\right)\)
=> Tứ giác GMAF n.t =>\(M\widehat{A}F+M\widehat{G}F=180^0\left(2\right)\)
(1) và (2) => \(N\widehat{G}F+M\widehat{G}F=180^0\)
=> \(\overline{M,G,N}\)
Mà G là giao điểm của AB và DF
Nên MN,AB,DF đồng quy tại G
MN là đường thẳng simson nha bạn
khong biet
a nha