Tìm m lớn nhất để hàm số \(\dfrac{1}{3}\)x3 – mx2 + (4m-3)x+2017 đồng biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 9 2019
Đáp án D
Ta có: y ' = x 2 − 2 m x + 4 m − 3 . Để hàm số đồng biến trên R thì y ' ≥ 0 ∀ x ∈ ℝ
⇔ Δ ' = m 2 − 4 m + 3 ≤ 0 ⇔ 1 ≤ m ≤ 3 ⇒ m lớn nhất bằng 3
CM
21 tháng 5 2019
Chọn B
Phương pháp:
Tính y', để hàm số đồng biến trên
ℝ
thì 
(y' = 0 tại hữu hạn điểm)
Sử dụng 
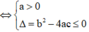
Cách giải:
Tập xác định D = ℝ
Đạo hàm 
Để hàm số đồng biến trên
ℝ
thì 
(y' = 0 tại hữu hạn điểm)
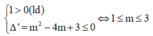
Suy ra giá trị lớn nhất của tham số m thỏa mãn ycbt là m = 3
CM
10 tháng 3 2019
Đáp án B
Ta có y ' = 3 x 2 + 2 m x + 1 − 2 m
Hàm số đồng biến trên − 3 ; 0 ⇔ y ' ≥ 0 , ∀ x ∈ − 3 ; 0 ⇔ 3 x 2 + 2 m x + 1 − 2 m ≥ 0 , ∀ x ∈ − 3 ; 0
⇔ m 2 x − 2 ≥ − 3 x 2 − 1 ⇔ m ≤ − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 1
Xét hàm số
f x = − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 ⇒ f ' x = − 6 x 2 + 12 x + 2 2 x − 2 2 ⇒ f ' x = 0 ⇔ x = 3 ± 2 3 3
Ta có bảng biến thiên hàm số f x như sau:
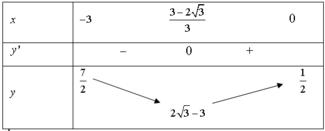
Suy ra f x − 3 ; 0 ≥ 2 3 − 3 ⇒ 1 ⇔ m ≤ 2 3 − 3
CM
13 tháng 11 2018
Đáp án A
Ta có: y ' = 3 x 2 + 2 m x − m .
Hàm số đồng biến trên ℝ ⇔ y ' ≥ 0 , ∀ x ∈ ℝ
⇒ Δ ' y ' ≤ 0 ⇔ m 2 + 3 m ≤ 0 ⇔ − 3 ≤ m ≤ 0.
\(y'=x^2-2xm+4m-3\)
Để hàm số đồng biến trên R \(\Rightarrow y'\ge0\) \(\forall x\in R\)
\(\Rightarrow x^2-2mx+4m-3\ge0\) \(\forall x\in R\)
\(\Rightarrow\Delta'=m^2-4m+3\le0\Rightarrow1\le m\le3\)
\(\Rightarrow GTLN\) của m để hs đồng biến trên R là \(m=3\)