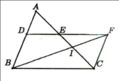
Cho tam giác đường thẳng song song với BC cắt AC ở E và đường thẳng kẻ từ C song song với AB cắt dường thẳng trước tại F. BF cắt AC tại S. Chứng minh SC^2 =SE.SA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 2 2019
nhầm đề bài rồi phải là SC^2 =SE.SA
20 tháng 2 2019
\(\frac{SE}{SC}=\frac{SC}{SA}\left(=\frac{SF}{SB}\right)\Rightarrow SC^2=SE.SA\)
17 tháng 5 2018
a. Vì FC // AB (gt)
=> \(\widehat{BAC}=\widehat{ECF}\left(soletrong\right)\)
Vì EF // BC (gt)
=> \(\widehat{FEC}=\widehat{ACB}\left(soletrong\right)\)
Xét \(\Delta CFE\) và \(\Delta ABC\) có:
\(\widehat{BAC}=\widehat{ECF}\) (cmt)
\(\widehat{FEC}=\widehat{ACB}\left(cmt\right)\)
Do đó: \(\Delta CFE\infty\Delta ABC\left(g-g\right)\)
b. Sử dụng tính chất của định lí Ta - lét
15 tháng 1 2022
a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)
