Tính chu vi tam giác ABC , biết độ dài các cạnh là AB= 15cm , BC = 25cm ,AC = 30 cm Giải giúp mình nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp giải:
Chu vi hình tam giác bằng tổng độ dài ba cạnh của hình đó.
Lời giải chi tiết:
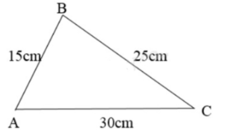
Chu vi hình tam giác ABC là:
15 + 25 + 30 = 70(cm)
Đáp số: 70cm.

Chu vi hình tam giác ABC là:
AB + BC + AC = 30 + 15 + 35 = 80 (cm)
Đáp số: 80cm

a)Xét ΔABC có: \(AB^2+AC^2=20^2+15^2=625\)
\(BC^2=25^2=625\)
=>ΔABC vuông tại A ( THEO ĐỊNH LÝ PYTAGO ĐẢO)
b)Xét ΔABH vuông tại H(gt)
=> \(AB^2=HB^2+AH^2\) (theo định lý pytago)
=> \(HB^2=AB^2-AH^2=20^2-12^2=256\)
=>HB =16
Có BC=BH+HC
=>HC=BC-BH=25-16=9
a) Xét \(\Delta ABC \) có:
\(BC^2=25^2=625\)
\(AB^2+AC^2=20^2+15^2=625\)
\(\Rightarrow BC^2=AB^2+AC^2\left(=625\right)\)
\(\Rightarrow\)\(\Delta ABC\) vuông tại A.
b) Xét \(\Delta ABH\) có: \(AH \perp BC\)
\(\Rightarrow\) \(AB^2=AH^2+BH^2\) (Định lí Pytago)
\(20^2=12^2+BH^2\left(AB=20cm\left(gt\right);AH=12cm\left(gt\right)\right)\)
\(\Rightarrow BH^2=20^2-12^2\)
\(BH^2=256\)
\(\Rightarrow BH=\sqrt{256}=16\left(cm\right)\)
Ta có:
\(BH+HC=BC\) (H nằm giữa B và C)
\(16+HC=25\left(BH=16cm\left(cmt\right);BC=25cm\left(gt\right)\right)\)
\(\Rightarrow HC=25-16\)
\(HC=9\left(cm\right)\)
Hình tam giác ABC có chu vi là (48cm ). Độ dài cạnh (AB = 15cm ) , (BC = 17cm ).
Độ dài cạnh AC là  cm
cm

Độ dài cạnh AC là:
48 – 15 – 17 = 16 (cm)
Số cần điền vào ô trống là 16

a)ta co : AB^2 + AC^2 = 20^2 +15^2 = 400 + 225 = 625 (cm)
BC = 25^2 = 625 (cm)
=> điều phải chứng minh
b) ta co : HC^2+HA^2 =AC^2
CH^2 = 15^2-12^2= 81cm
=> CH = 9cm
Lai co :
AH^2+BH^ = AB^2
12^2+BH^2 =20^2
144 + BH^2 = 400
BH^2 =256
=> BH =16cm

hình như có gì đó sai đề bạn ơi ! bạn xem kỹ lại bài toán đi !

Độ dài của cạnh AC là: 58-42=16(cm)
Độ dài của cạnh AB là: 58-34=24(cm)
Độ dài của cạnh BC là: 34-16=18(cm)
please :3
chu vi tam giác ABC là
15+25+30=70 cm
Bài giải
Chu vi hình tam giác là :
15 + 25 + 30 = 70 ( cm )
Đáp số : 70 cm
k mình nha ! Chúc bạn hok tốt