Cho tam giác ABC cân tại A. P và Q đối xứng nhau qua trung điểm của BC và PQ vuông góc AB. K là tâm ngoại tiếp tam giác APQ và AR là đường đối trung của tam giác APQ. KR, KC cắt phân giác góc PAQ tại M,N. Chứng minh rằng KM=KN ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 1 2018
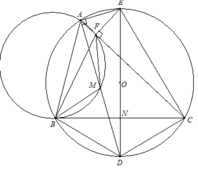
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C
CM
9 tháng 9 2018
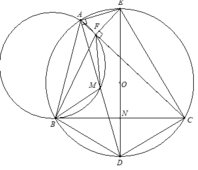
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).
NY
31 tháng 3 2020
Kẻ đường phân giác CJ của góc ACP cắt PE tại R mà không nói rõ J thuộc đương thẳng nào? đề khó hỉu quá anh(chị) ơi
NY
31 tháng 3 2020
a) Do P đối xứng B qua AC \(\Rightarrow\) \(\Delta\)APC đối xứng \(\Delta\)ABC qua AC \(\Rightarrow\) CR đối xứng CS qua AC ( vì CS là phân giác góc ACB) \(\Leftrightarrow\) R đối xứng S qua AC \(\Leftrightarrow\) RS\(\perp\)AC mà PB\(\perp\)AC \(\Leftrightarrow\) RS//PB
b) Do K đối xứng P qua CJ \(\Rightarrow\) CK đối xứng CP qua CJ \(\Leftrightarrow\) góc JCK = góc JCP = góc JCA ( vì CJ là phân giác góc ACP) \(\Rightarrow\)tia CK trùng tia CA \(\Rightarrow\) C; A; K thẳng hàng (1)
Cũng Do K đối xứng P qua CJ hay CR nên từ (1) \(\Rightarrow\) góc AKR = góc CKR = góc CPR = góc APR (2) ( vì PR là phân giác góc APC do BS là phân giác góc ABC vì \(\Delta\)APC đối xứng \(\Delta\)ABC qua AC)
Từ (2) \(\Rightarrow\) AKPR nội tiếp \(\Rightarrow\) AKBS nội tiếp ( vì đối xứng)
c) Gọi M là giao điểm của 2 tiếp tuyến tại K,P của (O) ⇒\(\Rightarrow\)M \(\in\) trung trực của KP (3)
Do K đối xứng P qua CJ \(\Leftrightarrow\) CJ là trung trực của KP (4)
Từ (3) và (4) ⇒ 2 tiếp tuyến tại K,P của (O) và CJ đồng quy tại M
ĐS:..................( đến đây thôi vì đề hơi kì xíu)
Gọi D là trung điểm BC. Kéo dài tia AR cắt đường tròn (K) tại điểm thứ hai S. Hạ đuờng thẳng KH vuông góc AS cắt BC ở I.
Do AR là đường đối trung của \(\Delta\)PAQ nên dễ thấy \(\Delta\)APD ~ \(\Delta\)ASQ => ^ADP = ^AQS.
Mà ^AQS = 1/2Sđ(AS = ^AKH nên ^ADP = ^AKH. Ta có: ^ADP = ^ACB (Để ý DP vuông góc AB)
Suy ra: ^AKH = ^ACB => Tứ giác AKIC nội tiếp => ^AKC = ^AIC (Góc ở 2 đỉnh liền kề) => ^AKN = ^AID (Kề bù) (1)
Xét đường tròn (K) có dây PQ, D là trung điểm PQ => KP vuông góc PQ => ^KDR = 900
Từ đó: Tứ giác KHRD nội tiếp. Ta cũng có: Tứ giác AIDH nội tiếp (AI) nên ^AID = ^DHR = ^DKR (2)
Từ (1) và (2) => ^AKN = ^DKR. Ta lại có:
^DAK = ^DAQ + ^KAQ = ^RAP + ^BAP (Dùng t/c đg đối trg và PQ vuông góc AB) = ^BAR
Dựa vào tính chất góc ngoài của tam giác: ^KNM = ^NAK + ^AKN = ^NAD + ^DAK + ^DKR
= ^NAR + ^BAR + ^DKR = ^NAR + 900 - ^ARP + 900 - ^DRK = ^NAR + 1800 - (^ARP + ^DRK)
= ^NAR + ^ARM = ^KMN. Vậy thì ^KNM = ^KMN => \(\Delta\)MKN cân đỉnh K => KM=KN (đpcm).