Tổng các nghiệm của phương trình 2cos3x(2cos2x+1)=1 trên đoạn \(\left[-4\pi,6\pi\right]\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=>2cos2x=pi(loại) hoặc sin x-cosx=0
=>sin x-cosx=0
=>sin(x-pi/4)=0
=>x-pi/4=kpi
=>x=kpi+pi/4
mà x\(\in\left[-pi;pi\right]\)
nên \(x\in\left\{\dfrac{pi}{4};-\dfrac{3}{4}pi\right\}\)
=> D

\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)

3.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=cos3x\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=sin\left(\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{2}-3x+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

\(\Leftrightarrow2cos^2\left(x+\dfrac{pi}{3}\right)-1=0\)
=>\(cos\left(2x+\dfrac{2}{3}pi\right)=0\)
=>2x+2/3pi=pi/2+kpi
=>2x=-1/6pi+kpi
=>x=-1/12pi+kpi/2
mà \(x\in\left(-\dfrac{pi}{2};\dfrac{5}{6}pi\right)\)
nên \(x\in\left\{-\dfrac{1}{12}pi;\dfrac{5}{12}pi\right\}\)


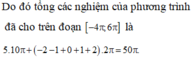
\(2cos3x\left(2-4sin^2x+1\right)=1\)
\(\Leftrightarrow2cos3x\left(3-4sin^2x\right)=1\)
Nhận thấy \(sinx=0\Leftrightarrow x=k\pi\) không phải nghiệm, nhân 2 vế của pt với \(sinx:\)
\(2cos3x\left(3sinx-4sin^3x\right)=sinx\)
\(\Leftrightarrow2cos3x.sin3x=sinx\)
\(\Leftrightarrow sin6x=sinx\Leftrightarrow\left[{}\begin{matrix}6x=x+k2\pi\\6x=\pi-x+l2\pi\end{matrix}\right.\) (chú ý \(x\ne m.\pi\))
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{7}+\dfrac{l2\pi}{7}\end{matrix}\right.\) ; \(x\ne m.\pi\)
Xét trên \(\left[-4\pi;6\pi\right]\): \(\left\{{}\begin{matrix}-4\pi\le\dfrac{k2\pi}{5}\le6\pi\\-4\pi\le\dfrac{\pi+l2\pi}{7}\le6\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-10\pi\le k\le15\pi\\-13\le l\le20\pi\end{matrix}\right.\)
Vậy tổng các nghiệm:
\(S=\pi\left(\sum\limits^{15}_{k=-10}\dfrac{2k}{5}+\sum\limits^{20}_{l=-13}\dfrac{2l+1}{7}-\sum\limits^6_{m=-4}m\right)=\dfrac{377.\pi}{7}\)