Giúp em bài 1 2 4 gấp với...
Đọc tiếp
Giúp em bài 1 2 4 gấp với :(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2021
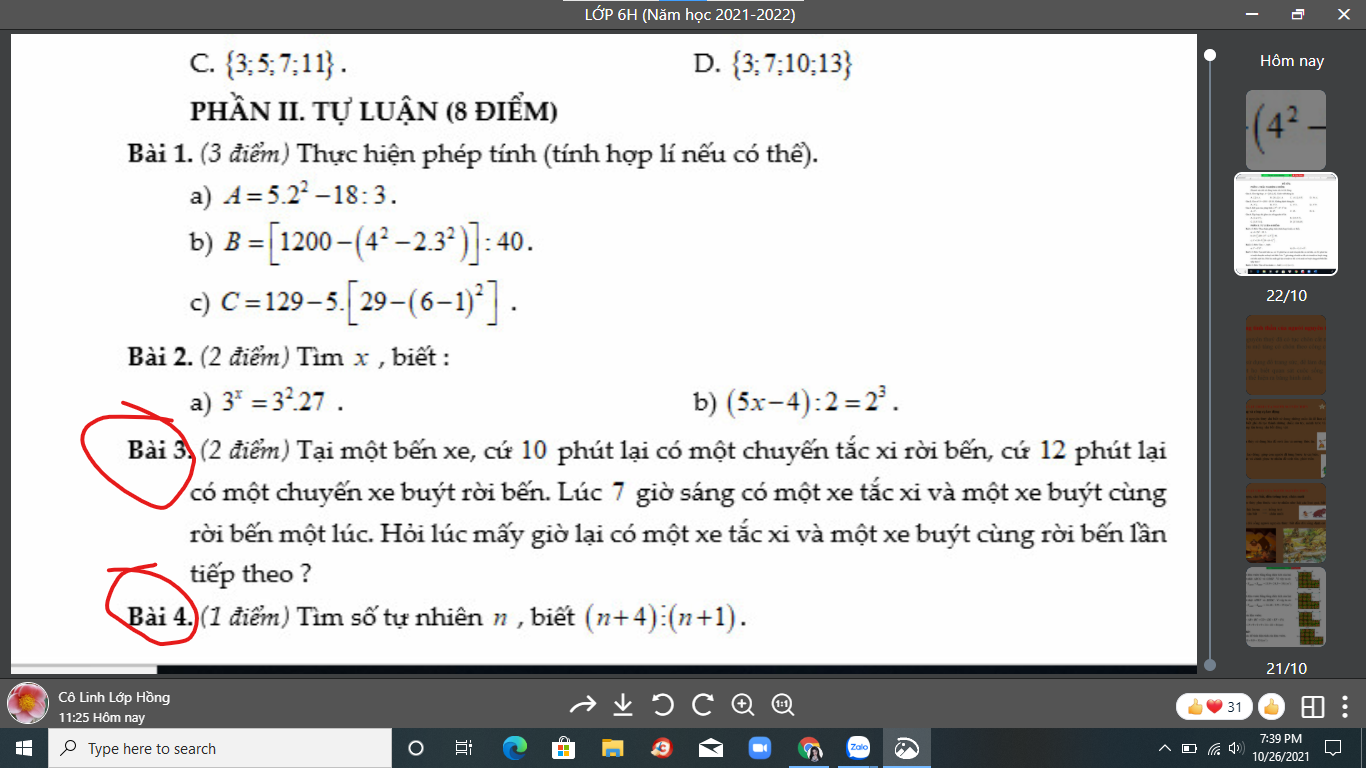
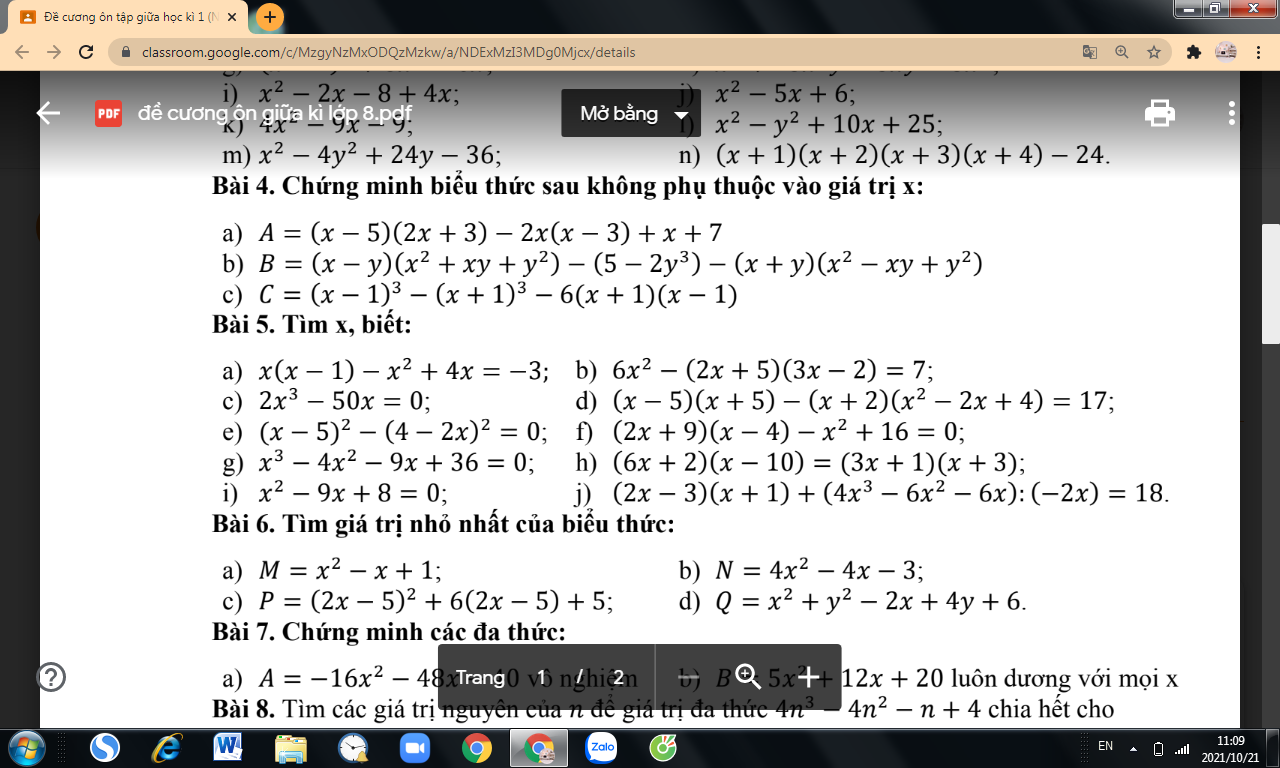
Bài 4:
\(\Leftrightarrow n+1\in\left\{1;3\right\}\)
hay \(n\in\left\{0;2\right\}\)
26 tháng 10 2021
\(\left(n+4\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+3⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Mà \(n\in N\)
\(\Rightarrow n\in\left\{0;2\right\}\)
21 tháng 10 2021
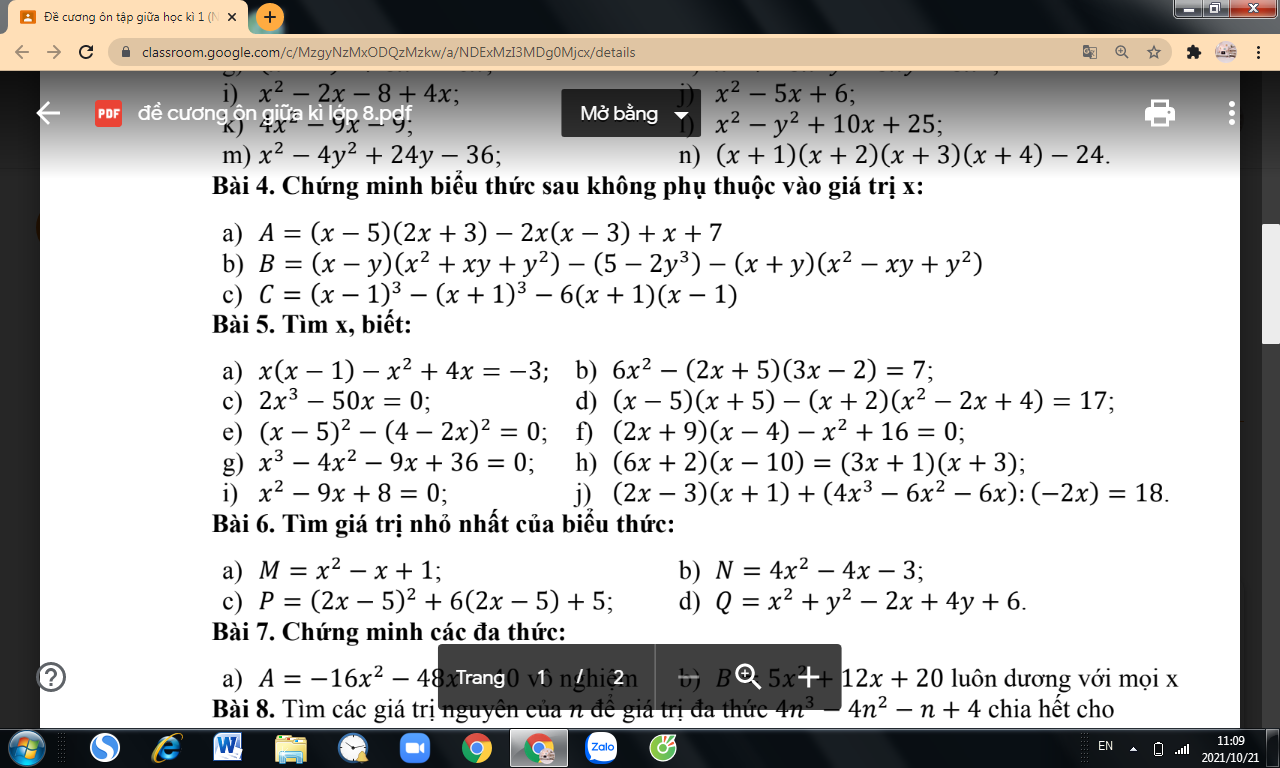
Bài 4:
b: \(B=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3-5-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3-y^3+2y^3-5-x^3-y^3\)
=-5
c: \(C=\left(x-1\right)^3-\left(x+1\right)^3-6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6\left(x^2-1\right)\)
\(=-6x^2-2-6x^2+6\)
\(=-12x^2+4\)
21 tháng 10 2021
Bài 4:
\(A=2x^2+3x-10x-15-2x^2+6x+x+7=-8\\ B=x^3-y^3-5+2y^3-x^3-y^3=-5\\ C=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+6=4\)
LC
0
3 tháng 10 2021
câu 4:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=6(cm)
b: Xét ΔBAC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
nên \(AM=\dfrac{BC}{2}=6.5\left(cm\right)\)
NT
1
24 tháng 7 2021
3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)
bạn chụp thế này thì chết rồi
bruh so hard
:v