tìm m để hàm số y= X3 - (2m-3)X2 - (4m-15)x -5 có cực trị
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TL
1
Những câu hỏi liên quan
CM
19 tháng 12 2018
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 
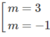
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
PT
Tìm giá trị của tham số m để hàm số y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1
1
CM
23 tháng 9 2018
y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = − m + 1 2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − m + 1 2 + 4 = 0 ⇔ m + 1 2 = 4
⇔ 
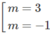
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
CM
4 tháng 3 2018
Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)
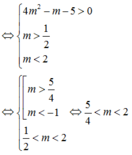
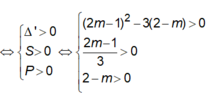
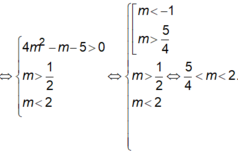
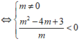
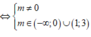
y'=3x2-2(2m-3)x-(4m-15)
để hs y có cực trị thì y'=0 có 2 nghiệm phân biệt
Δ,=(2m-3)2-3(4m-15)>0
<=> 4m2-24m+54>0
<=>(2m-6)2+18>0 với mọi m
=> hs luôn có cực trị với mọi m
sai rồi b ơi