vào luúc 10h sáng tia nắng chia tạo thành 1 góc 60 đooj, ngta thấy bóng của 1 cây đối xứng là 2m. hỏi cây cao bao nhiêu (bài toán thực tế)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Một cây gậy cao 1m có bóng là 60cm. Khi đó, tỉ lệ giữa bóng và chiều cao thật là: \(60:100=60\%\)
\(\Rightarrow\) Chiều cao của cây gậy là: \(100:60\%=166\dfrac{2}{3}\left(m\right)\)
Đáp án: \(166\dfrac{2}{3}m\)
Mong cái này giúp được bạn nhé.☺

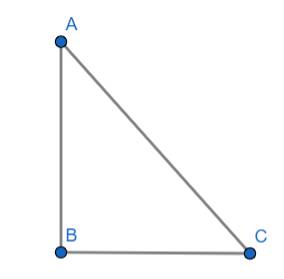
Với AB là chiều cao cây, BC là bóng cây, góc tạo bởi mặt trời và mặt đất là góc C
Ta có: \(tanC=\dfrac{AB}{BC}\)
\(\Rightarrow tanC=\dfrac{3}{2}\)
\(\Rightarrow\widehat{C}\approx56^o\)
Vậy góc tạo bởi mặt trời và mặt đất là 56o

Đáp án: ≈12 mét
Giải thích các bước giải:
Chiều cao của cây là 20.tan31≈12mét
\(\tan (C) = \dfrac{AB}{AC} \) ⇔ \(\tan (33) = \dfrac{AB}{40}\) ⇔ \(AB \) \(= 25,9 m\)

Đổi: 2m 10 cm = 2,1 m
1 m 40 cm = 1,4 m
4m 20 cm = 4,2 m
Chiều cao của cái cây là:
4,2 : 1,4 x 2,1 = 6,3 (m)
Đổi: 2m 10 cm = 2,1 m
1 m 40 cm = 1,4 m
4m 20 cm = 4,2 m
Chiều cao của cái cây là:
4,2 x 2,1 : 1,4 = 3 (m)

Chiều cao của cây là
\(\frac{h_{nam}}{h_{cây}}=\frac{d_{nam}}{d_{cây}}\)( d là độ dài bóng, h là chiều cao)
\(\Leftrightarrow\frac{1,5}{h_{cây}}=\frac{2}{12}\)
\(\Leftrightarrow h_{cây}=\frac{1,5.12}{2}=9\left(m\right)\)

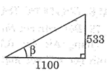
Chiều cao của đài quan sát là cạnh góc vuông đối diện với góc nhọn, bóng của nó trên mặt đất là cạnh góc vuông kề với góc nhọn
Ta có: tg β = 533/1100 ≈ 0,4845
Suy ra: β ≈ 25 ° 51 '
Vậy góc tạo bởi tia sáng mặt trời và mặt đất là 25 ° 51 '

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)