Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

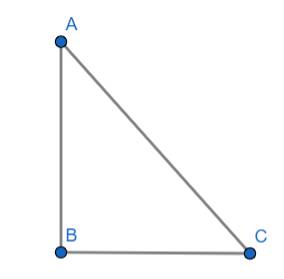
Với AB là chiều cao cây, BC là bóng cây, góc tạo bởi mặt trời và mặt đất là góc C
Ta có: \(tanC=\dfrac{AB}{BC}\)
\(\Rightarrow tanC=\dfrac{3}{2}\)
\(\Rightarrow\widehat{C}\approx56^o\)
Vậy góc tạo bởi mặt trời và mặt đất là 56o

Đáp án: ≈12 mét
Giải thích các bước giải:
Chiều cao của cây là 20.tan31≈12mét
\(\tan (C) = \dfrac{AB}{AC} \) ⇔ \(\tan (33) = \dfrac{AB}{40}\) ⇔ \(AB \) \(= 25,9 m\)

Chiều cao của đài quan sát là cạnh góc vuông đối diện với góc nhọn, bóng của nó trên mặt đất là cạnh góc vuông kề với góc nhọn
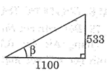
Ta có: tg β = 533/1100 ≈ 0,4845
Suy ra: β ≈ 25 ° 51 '
Vậy góc tạo bởi tia sáng mặt trời và mặt đất là 25 ° 51 '

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)

Gọi AC là chiều cao của cây, AB là bóng của cây trên mặt đất
Theo đề, ta có: AB vuông góc với AC tại A, AB=8,1m; \(\widehat{B}=55^0\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(AC=8.1\cdot tan55\simeq11,57\left(m\right)\)

Xét tam giác ABC vuông tại A có:
\(tanC=\dfrac{533}{1100}\approx0,4845\Rightarrow C\approx25^o51'\)

Chiều cao của cái cây đó là:
4,5*tan55\(\simeq6,43\left(m\right)\)