Hỏi AB có song song với EF không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
30 tháng 1 2021
a/ Có AB // DM
=> t/g ABE đồng dạng t/g MDE (đ/l)
=> AE/ME = AB/MD = AB/MC (1)
Có AB // CM
=> t/g ABF đồng dạng t/g CMF (đ/l)
=> AF/MF = AB/CM (2)(1) ; (2)
=> AE/ME = AF/MF
Xét t/g AMB có AE/ME=AF/MF
=> EF // BC (Thales đảo)
b/ Xét t/g DEM có AB // DM
=> ME/AM = DM/AB (Hệ quả đ.l Thales)
Xét t/g AMB có EF // AB
=> ME/AM = EF/AB (Hệ quả Thales)
Do đó EF = DM = 1/2DC = 6 (cm)P/s: câu b không chắc lắm.
30 tháng 1 2021
a) Ta có: AB//CD(AB và CD là hai đáy của hình thang ABCD)
nên AB//MC
Xét ΔAFB và ΔCFM có
\(\widehat{FAB}=\widehat{FCM}\)(hai góc so le trong, AB//MC)
\(\widehat{AFB}=\widehat{CFM}\)(hai góc đối đỉnh)
Do đó: ΔAFB\(\sim\)ΔCFM(g-g)
nên \(\dfrac{FA}{FC}=\dfrac{FB}{FM}=\dfrac{AB}{CM}\)
mà CM=DM(M là trung điểm của CD)
nên \(\dfrac{BF}{FM}=\dfrac{AB}{DM}\)(1)
Ta có: AB//CD(Hai cạnh đáy của hình thang ABCD)
nên AB//DM
Xét ΔABE và ΔMDE có
\(\widehat{ABE}=\widehat{MDE}\)(hai góc so le trong, AB//DM)
\(\widehat{AEB}=\widehat{MED}\)(hai góc đối đỉnh)
Do đó: ΔABE\(\sim\)ΔMDE(g-g)
nên \(\dfrac{AB}{DM}=\dfrac{AE}{EM}\)(2)
Từ (1) và (2) suy ra \(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)
Xét ΔAMB có
E\(\in\)AM(Gt)
F\(\in\)BM(gt)
\(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)(cmt)
Do đó: EF//AB(Định lí Ta lét đảo)
10 tháng 4 2022
a) Nối A với F 
Và D với F
Ta có:
ED=1/3 AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
CM
1 tháng 12 2019
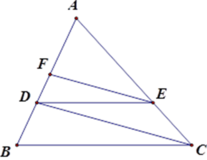
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C
25 tháng 10 2021
a: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
b: \(BC=2\cdot EF=2\cdot5=10\left(cm\right)\)
25 tháng 10 2021
a) Xét tam giác ABC có:
M là trung điểm BC
ME//AC
=> E là trung điểm AB
Xét tam giác ABC có:
M là trung điểm BC
MF//AB
=> F là trung điểm AC
Xét tam giác ABC có:
E là trung điểm AB(cmt)
F là trung điểm AC(cmt)
=> EF là đường trung bình
c) Ta có: EF là đường trung bình
\(\Rightarrow BC=2EF=2.5=10\left(cm\right)\)
AB có song song với EF nhé
HT
BẠN NHÉ
Hỏi AB có song song với EF không?
AB có song song với EF