BÀI 3.Cho tam giácABCđều cạnha. Tính bán kính đường tròn đi qua ba điểmA,B,C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 9 2021
Tâm của ba đường tròn này sẽ nằm trên đường trung trực của AB
ND
Nguyễn Đức Trí
VIP
7 tháng 9 2023
Xét \(\Delta\) vuông tại H \(ABH\) có :
\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)
Xét \(\Delta\) vuông tại H \(ACH\) có :
\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)
\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)
Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC
\(\Rightarrow\) Bán kính đường tròn này là :
\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)
CM
12 tháng 3 2017
Vì tam giác ABC là tam giác đều nên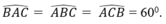 
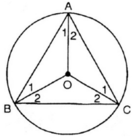
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
* Xét tam giác AOB có:
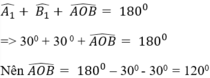
* Tượng tự ta được: 
HH
19 tháng 1 2021
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)
1 tháng 9 2023
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=12^2+16^2=400
=>BC=20
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C\(\simeq\)37 độ
=>góc B=53 độ
ΔABC vuông tại A
=>A,B,C cùng nằm trên đường tròn đường kính BC
=>R=BC/2=20/2=10
Bán kính là:
\(R=\dfrac{2a\sqrt{3}}{3}\)