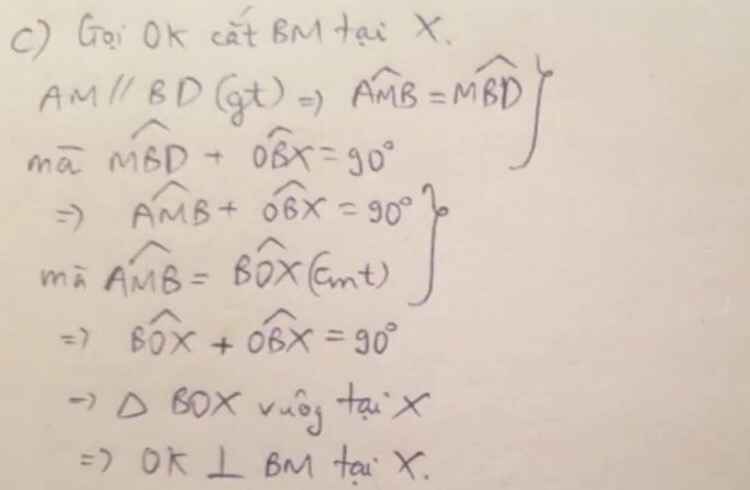mấy bài khoanh đỏ ạ
mấy bài khoanh đỏ ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 11:
a) \(A=\left(x-47\right)-\left(x+59-81\right)+\left(35-x\right)\)
\(A=x-47-x-59+81+35-x\)
\(A=\left(x-x-x\right)+\left(-47-59+81+35\right)\)
\(A=x\cdot\left(1-1-1\right)-34\)
\(A=-x-34\)
b) \(B=x-34-\left[\left(15+x\right)-\left(23-x\right)\right]\)
\(B=x-34-\left(15+x-23+x\right)\)
\(B=x-34-\left(2\cdot x-8\right)\)
\(B=x-34-2\cdot x+8\)
\(B=-x-26\)
c) \(C=\left(71+x\right)-\left(-24-x\right)+\left(-35-x\right)\)
\(C=71+x+24+x-35-x\)
\(C=\left(x+x-x\right)+\left(71+24-35\right)\)
\(C=x\cdot\left(1+1-1\right)+60\)
\(C=x+60\)
Bài 14:
a) Diện tích sàn nhà cùa Phát là:
\(10\cdot8=80\left(m^2\right)\)
b) Đổi: 50 cm = 0,5 m
Diện tích của mỗi viên gạch là:
\(0,5\cdot0,5=0,25\left(m^2\right)\)
Số viên gạch cần dùng để lát sàn nhà của Phát là:
\(80:0,25=320\) (viên)

Bài 32a
Thay x = -3 vào ta được
\(18+3m^2+18m=0\Leftrightarrow m=-3\pm\sqrt{3}\)
Bài 33b
\(\Delta'=4m^2-\left(4m-1\right)\left(m+1\right)=4m^2-4m^2-3m+1=1-3m\)
Để pt có 2 nghiệm pb \(1-3m>0\Leftrightarrow m< \dfrac{1}{3}\)

(Dòng khoanh đỏ ở dấu tương đương đầu tiên)Có nghĩa là chia cả hai vế cho \(\dfrac{5\pi}{3}\) ấy
(Dòng khoanh đỏ ở dấu tương đương thứ hai) Xét \(cos\pi x=\dfrac{1}{10}+k\dfrac{6}{5}\) (*)
Do \(-1\le cos\pi x\le1\)\(\Leftrightarrow-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\)
\(\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{3}{4}\) mà k nguyên \(\Rightarrow k=0\)
Thay k=0 vào (*)\(\Rightarrow cos\pi x=\dfrac{1}{10}\)
Làm tương tự với cái bên dưới \(-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\) \(\Leftrightarrow-\dfrac{5}{4}\le k\le\dfrac{5}{12}\Rightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\)
Thay k=0 với k=-1 sẽ ra được \(\left[{}\begin{matrix}cos\pi x=\dfrac{1}{2}\\cos\pi x=-\dfrac{7}{10}\end{matrix}\right.\)
(Với mỗi \(cos\pi x\) sẽ nhận được hai họ nghiệm => Tổng tất cả là 6 họ nghiệm)
Vì \(cosx\in\left[-1;1\right]\Rightarrow\left[{}\begin{matrix}-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\left(1\right)\\-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{9}{12}\Leftrightarrow k=0\Rightarrow cosx=\dfrac{1}{10}\)
\(\left(2\right)\Leftrightarrow-\dfrac{15}{12}\le k\le\dfrac{5}{12}\Leftrightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{7}{10}\end{matrix}\right.\)

9:
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-2m+4\right)\)
=4m^2-4m^2+8m-16=8m-16
Để phương trình có hai nghiệm phân biệt thì 8m-16>0
=>m>2
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+4)-2m=8
=>4m^2-2m^2+4m-8-2m=8
=>2m^2+2m-16=0
=>m^2+m-8=0
mà m>2
nên \(m=\dfrac{-1+\sqrt{33}}{2}\)


M=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{x-1}\right)\)
=\(\dfrac{\left(\sqrt{x}\cdot\sqrt{x}\right)-1}{\sqrt{x\left(\sqrt{x}-1\right)}}:\dfrac{\sqrt{x}-1+2}{x-1}\)
=\(\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}\)
=\(\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{x-1}{\sqrt{x+1}}\)
=\(\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
=\(\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(x-1\right)}\)
=\(\dfrac{x-1}{\sqrt{x}}=\dfrac{\sqrt{x}\left(x-1\right)}{x}\)

Bài 2:
a: Ta có: \(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
\(=\dfrac{x-1}{x}\)
b: Để P>1/2 thì P-1/2>0
\(\Leftrightarrow\dfrac{x-1}{x}-\dfrac{1}{2}>0\)
\(\Leftrightarrow2x-2-x>0\)
=>x>2


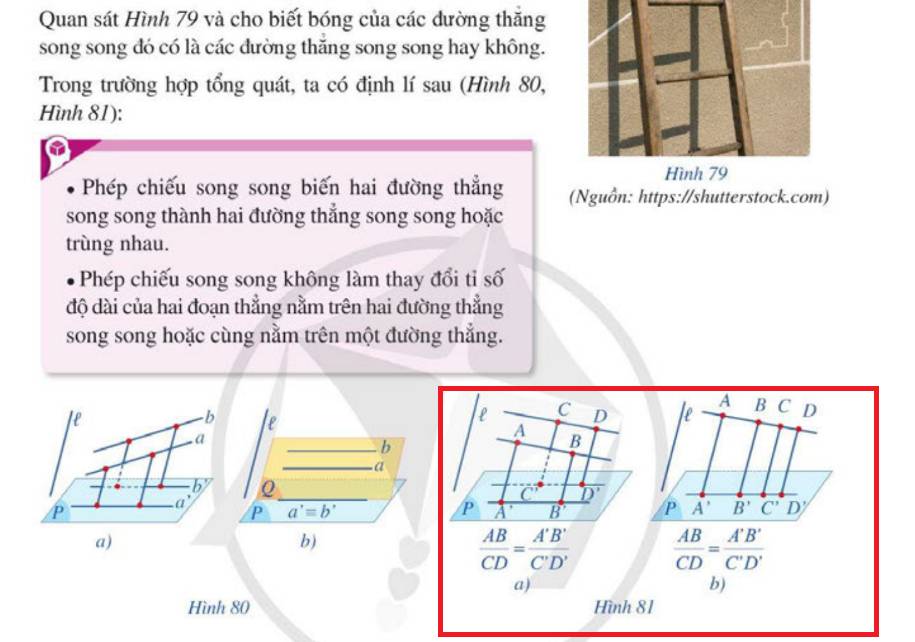
Ở hình a, em sử dụng 1 đường thẳng song song AB và CD qua B' và D' lần lượt cắt AA' và CC' tại E và F
Khi đó 2 tam giác A'B'E và C'D'F đồng dạng (3 cặp cạnh song song) nên dễ dàng suy ra đpcm
Hình b tương tự, chỉ cần qua D' kẻ 1 đường song song AD rồi lại đồng dạng là xong