Cho tam giác ABC cân tại A có AH là đường cao và D la trung điểm cạnh AC.Gọi E là điểm đối xứng với H QUA D
A. CHỨNG MINH TỨ GIÁC AHCE LA HINH CHỮ NHẬT
B.HE=AB
C.GỌI G LÀ GIAO ĐIỂM CỦA BD VÀ AH.ĐƯỜNG CAO CG CẮT AB TẠI F. CHỨNG MINH EF//BG
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác AHCE có
AD = DC
HD = DE
=> AHCE là hình bình hành
H =90°
=> AHCE là hình chữ nhật
b) Vì ∆ABC cân tại A
=>AB = AC
Mà AC = HE (AHCE là hình chữ nhật)
=> AB = HE
Mình mới làm tới câu b thôi

a, tứ giác AHCE là hình chữ nhật , vì AD=DC và HD=DE
b, áp dụng đl pytago vào tam giác vuông AHC( H là đường cao ABC):
\(HC^2=AC^2-AH^2\\ HC^2=10^2-6^2\\ HC=\sqrt{10^2-6^2}=8cm\)
\(S_{AHCE}=AH.HC=6.8=48cm^2\)

a: Xét tứ giác AHCE có
D là trung điểm chung của AC và HE
góc AHC=90 độ
Do đó: AHCE là hình chữ nhật
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
=>BC=2*BH=6cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)

a/
Ta có
IA=IC (gt)
IH=IE (gt)
=> AHCE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
\(AH\perp BC\Rightarrow\widehat{AHC}=90^o\)
=> AHCE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)
b/
Xét tg AHC có
MH=MC (gt)
IA=IC (gt)
=> G là trong tâm của tg AHC \(\Rightarrow HG=2IG\) (1)
\(\Rightarrow HG+IG=IH=3IG\) (2)
Chứng minh tương tự ta có K là trọng tâm của tg ACE
\(\Rightarrow KE=2IK\left(3\right)\Rightarrow KE+IK=IE=3IK\) (4)
Mà IH=IE (gt) (5)
Từ (2) (4) (5) => IG=IK (6)
Từ (1) (3) (6) => HG=KE
Mà IG=IK => IG+IKGK=2IK=KE
=> HG=GK=KE

a: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật

a)Bn c/m AEBH là hbh (2 đchéo cắt tại trđiểm mỗi đường) rồi có góc H vuông nên là hcn
b)từ hcn ta có EH=AB, mà Ab=AC
=>EH=AC
c)ta có EH=ac, ea=HC(cùng bằng BH)
=>EACH là hbh
=>EH//AC
tứ giác EFCD có
ED//FC
ED=FC(cùng bằng AD)
nên EFCD là hbh
=>EF//CD
mà G nằm trên CD
>EF//CG

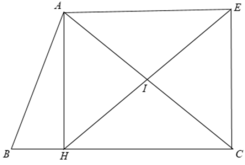
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.
(Hình bạn tự vẽ nhé)
a)
Tứ giác AHCE có:
AD = DC
HD = DE
=> AHCE là hình bình hành
mà ^AHC = 90o => AHCE là hình chữ nhật.
b)
AHCE là hình chữ nhật => HE = AC
mà AC = AB (tam giác ABC cân ở A)
=> HE = AB
c)
\(\Delta ABC:CF\perp AD,AH\perp BC\)
mà CF giao AH tại G => G là trực tâm => \(BD\perp AC\)(1)
Tứ giác AEDF có:
AE = DF ( = 1/2 BC - tự c/m đường trung bình nhé)
AF = ED ( = 1/2 AB - cmtt)
=> Tứ giác AEDF là hình thoi => \(AD\perp EF\)(2 đường chéo vuông góc với nhau) (2)
Từ (1) và (2) => EF//BD (đpcm)
Chúc bạn học tốt!!!