chứng minh bất đẳng thức Nesbitt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
13 tháng 7 2020
C3
Đặt \(S=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\)
\(M=\frac{b}{b+c}+\frac{c}{c+a}+\frac{a}{a+b}\)
\(N=\frac{c}{b+c}+\frac{a}{c+a}+\frac{b}{a+b}\)
Ta có : \(M+N=\left(\frac{b}{b+c}+\frac{c}{c+a}+\frac{a}{a+b}\right)+\left(\frac{c}{b+c}+\frac{a}{c+a}+\frac{b}{a+b}\right)\)
\(=\left(\frac{b}{b+c}+\frac{c}{b+c}\right)+\left(\frac{c}{c+a}+\frac{a}{c+a}\right)+\left(\frac{a}{a+b}+\frac{b}{a+b}\right)\)
\(=\frac{b+c}{b+c}+\frac{c+a}{c+a}+\frac{a+b}{a+b}=1+1+1=3\)
Ta có :\(+)M+S=\frac{b}{b+c}+\frac{c}{c+a}+\frac{a}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\)
\(=\frac{b+a}{b+c}+\frac{c+b}{c+a}+\frac{a+c}{b+a}\)
Hoàn toàn tương tự :\(+)N+S=\frac{a+c}{b+c}+\frac{b+a}{c+a}+\frac{b+c}{b+a}\)
Áp dụng Bất đẳng thức Cauchy cho 2 số không âm ta được :
\(\frac{b+a}{b+c}+\frac{c+b}{c+a}+\frac{a+c}{b+a}\ge3\sqrt[3]{\frac{\left(b+a\right)\left(c+b\right)\left(a+c\right)}{\left(b+c\right)\left(c+a\right)\left(b+a\right)}}=3\)
\(\frac{a+c}{b+c}+\frac{b+a}{c+a}+\frac{b+c}{b+a}\ge3\sqrt[3]{\frac{\left(a+c\right)\left(b+a\right)\left(b+c\right)}{\left(b+c\right)\left(c+a\right)\left(b+a\right)}}=3\)
Cộng theo vế các bất đẳng thức cùng chiều ta được :
\(M+N+2S\ge3+3=6\)
\(< =>3+2S\ge6< =>2S\ge6-3=3< =>S\ge\frac{2}{3}\)
Vậy ta có điều phải chứng minh
9 tháng 7 2020
\(P=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{b+a}=\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}-3\)
\(=\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)-3\)
\(\ge\left(a+b+c\right)\frac{9}{b+c+a+c+a+b}-3\)
\(=\frac{9}{2}-3=\frac{3}{2}\)
Dấu "=" xảy ra <=> a = b = c
HN
28 tháng 3 2017
Có nhiều cách lắm. T đơn cử 1 cách nhé
\(\sum\dfrac{a}{b+c}=\sum\dfrac{a^2}{ab+bc}\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
NH
29 tháng 3 2017
\(A=\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\)
3+A=\(\dfrac{a}{b+c}+1+\dfrac{b}{a+c}+1+\dfrac{c}{a+b}+1\)
3+A=\(\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}+\dfrac{1}{a+b}\right)\)
đặtx=a+b;y=a+c;z=b+c
=>3+A=\(\dfrac{1}{2}\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
mà (x+y+z)(\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\))\(\ge\)9
=>3+A\(\ge\dfrac{9}{2}\)
=>A\(\ge\dfrac{3}{2}\)
TM
4
AH
Akai Haruma
Giáo viên
23 tháng 1 2022
Lời giải:
Bổ sung điều kiện $a,b$ là các số dương. Áp dụng BĐT Cô-si ta có:
$a+b\geq 2\sqrt{ab}$
$\frac{1}{a}+\frac{1}{b}\geq 2\sqrt{\frac{1}{ab}}$
$\Rightarrow (a+b)(\frac{1}{a}+\frac{1}{b})\geq 2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4$
Ta có đpcm
Dấu "=" xảy ra khi $a=b$
CM
26 tháng 6 2018
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)
= x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Ta có: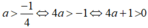 
Tương tự. 4b +1 >0 và 4c +1 > 0
Áp dụng bất đẳng thức Cô-si cho hai số dương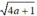 
và 1 ta có:
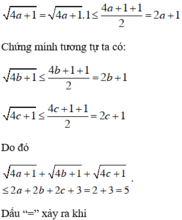
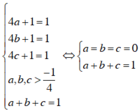
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.
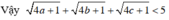
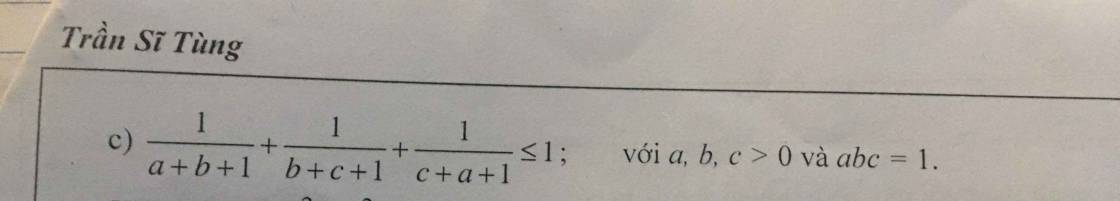
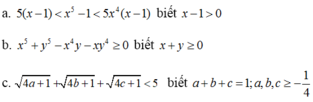
vào đường link này nè bạn!
45-cach-chung-minh-bdt-nesbitt.pdf
https://trungtuan.files.wordpress.com/2011/01/45-cach-chung-minh-bdt-nesbitt.pdf
Vào đây nè.
https://trungtuan.files.wordpress.com/2011/01/45-cach-chung-minh-bdt-nesbitt.pdf