tìm số nguyên n sao cho 4n+9 chia hết cho 2n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
HT
1

BT
28 tháng 2 2018
4n-9 = 4n+2-11 = 2(2n+1)-11. Nhận thấy: 2(2n+1) chia hết cho 2n+1 với mọi n
=> Để (4n-9) chia hết cho 2n+1 thì 11 phải chia hết cho 2n+1
=> 2n+1 = (-11,-1,1,11)
| 2n+1 | -11 | -1 | 1 | 11 |
| n | -6 | -1 | 0 | 5 |
NN
0

HA
1


18 tháng 7 2021
`4n+3 vdots 2n+1`
`=>4n+2+1 vdots 2n+1`
`=>2(2n+1)+1 vdots 2n+1`
`=>1 vdots 2n+1`
`=>2n+1 in Ư(1)={1,-1}`
`*2n+1=1=>2n=0=>n=0(tm)`
`*2n+1=-1=>2n=-2=>n=-1(tm)`
Vậy `n in {0;-1}` thì `4n+3 vdots 2n+1`
18 tháng 7 2021
\(4n+3⋮2n+1\Leftrightarrow2\left(2n+1\right)+1⋮2n+1\Leftrightarrow1⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(1\right)=\left\{\pm1\right\}\)
| 2n + 1 | 1 | -1 |
| n | 0 | -1 |

4 tháng 1 2022
a: \(\Leftrightarrow2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2;-1\right\}\)
c: \(\Leftrightarrow n+1\in\left\{1;-1\right\}\)
hay \(n\in\left\{0;-2\right\}\)
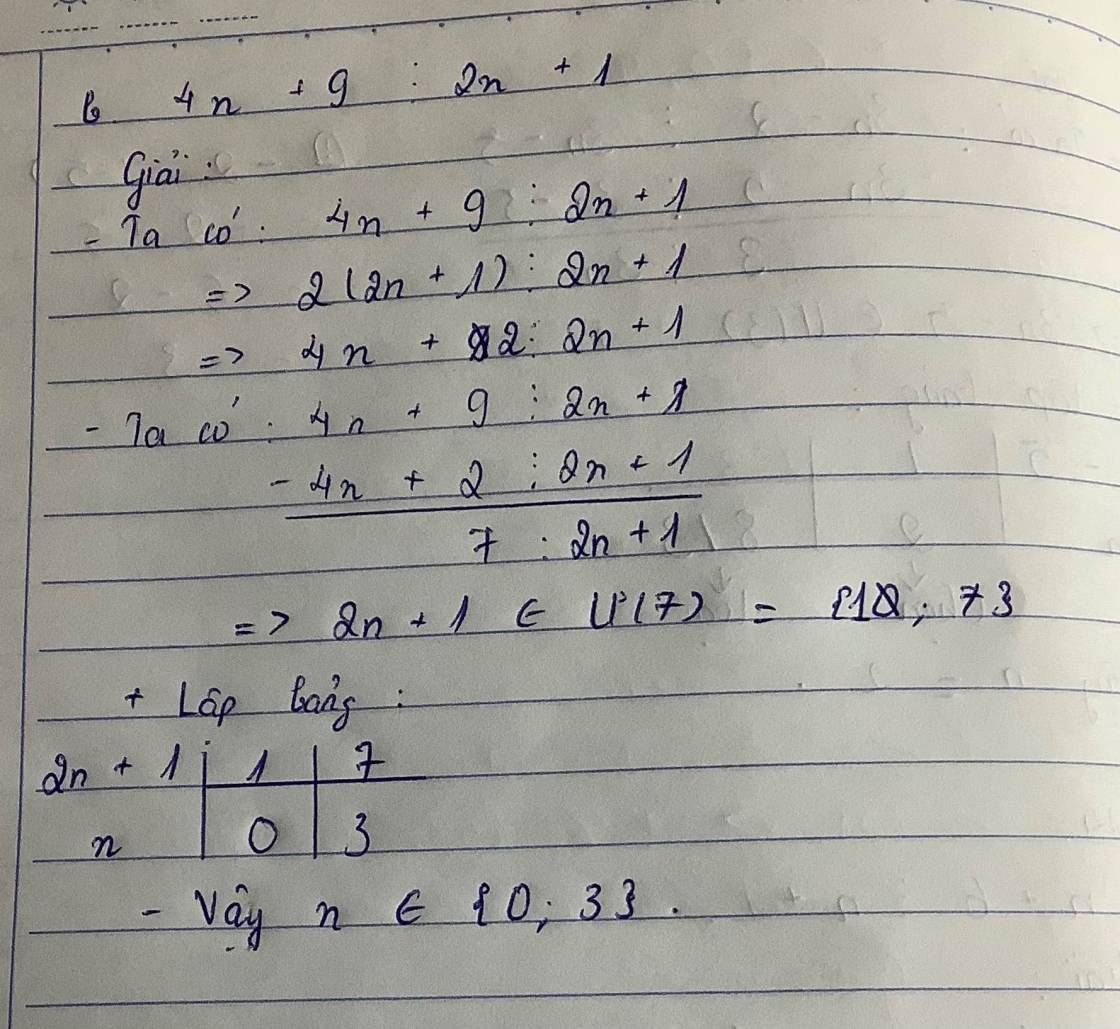
\(4n+9=4n+2+7=2\left(2n+1\right)+7\)chia hết cho \(2n+1\)
tương đương với \(7\div\left(2n+1\right)\)mà \(n\)nguyên nên
\(2n+1\inƯ\left(7\right)=\left\{-7,-1,1,7\right\}\)
\(\Leftrightarrow n\in\left\{-4,-1,0,3\right\}\).