cho tam giác nhọn ABC đường cao AH. gọi M, N, P là trung điểm AB, AC, BC. tứ giác MNPH là hình gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
Lời giải:
$M,N$ lần lượt là trung điểm $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow MN\parallel BC$ hay $MN\parallel HP$
$\Rightarrow MNPH$ là hình thang $(*)$
Mặt khác:
Tam giác vuông $ABH$ có $HM$ là đường trung tuyến ứng với cạnh huyền nên $HM=\frac{AB}{2}=MB$ (bổ đề quen thuộc)
$\Rightarrow $MHB$ cân tại $M$
$\Rightarrow \widehat{MHB}=\widehat{MBH}$
Mà $\widehat{MBH}=\widehat{NPC}$ (hai góc đồng vị với $NP\parallel AB$)
$\Rightarrow \widehat{MHB}=\widehat{NPC}$
$\Rightarrow 180^0-\widehat{MHB}=180^0-\widehat{NPC}$
Hay $\widehat{MHP}=\widehat{NPH}(**)$
Từ $(*); (**)\Rightarrow $MNPH$ là hình thang cân (đpcm)
13 tháng 9 2023
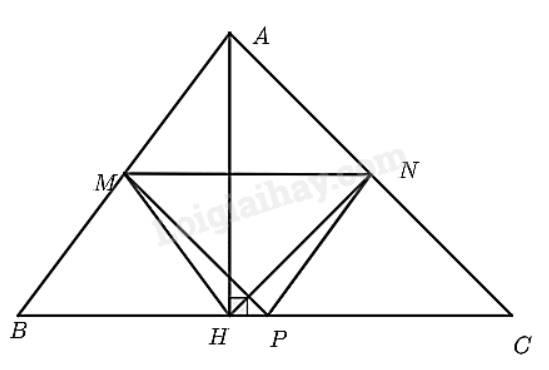
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).
\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)
Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.
- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).
- Xét tam giác \(AHC\) vuông tại \(H\) có:
\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).
Từ (1) và (2) suy ra \(MP = HN\).
Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).
Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).
22 tháng 10 2023
a: Xét tứ giác APCQ có
N là trung điểm chung của AC và PQ
nên APCQ là hình bình hành
=>AQ//CP và AQ=CP
AQ=CP
CP=PB
Do đó: AQ=BP
AQ//CP
mà B thuộc tia đối của tia CP
nên AQ//BP
Xét tứ giác AQPB có
AQ//PB
AQ=PB
Do đó: AQPB là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC
=>MN//HP
Xét ΔABC có
M,P lần lượt là trung điểm của BA,BC
=>MP là đường trung bình
=>MP//AC và MP=AC/2(1)
ΔAHC vuông tại H
mà HN là đường trung tuyến
nên \(HN=\dfrac{AC}{2}\)(2)
Từ (1),(2) suy ra MP=HN
Xét tứ giác MNPH có
MN//PH
MP=HN
Do đó: MNPH là hình thang cân
16 tháng 10 2021
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
hay MN//HP
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của BC
Do đó: MP là đường trung bình của ΔACB
Suy ra: \(MP=\dfrac{AC}{2}\left(1\right)\)
Ta có: ΔAHC vuông tại H
mà HN là đường cao ứng với cạnh huyền AC
nên \(HN=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MP=HN
Xét tứ giác MNPH có MN//PH
nên MNPH là hình thang
mà MP=HN
nên MNPH là hình thang cân