Cho góc xOy. Trên tia Ox lấy hai điểm A, B (OA<OB). Trên tia Oy lấy hai điểm C,D sao cho OC=OA, OD=OB.Gọi I là giao điểm của AD và BC.Chúng minh rằng :
a,tam giác OAD=tam giácOCB
b,OI là tia phân giác của góc xOy
c,AC//BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

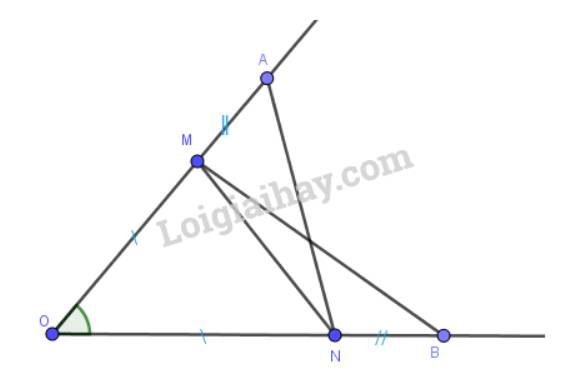
a) Xét \(\Delta OAN\) và \(\Delta OBM \) có:
OA=OB (gt)
\(\widehat{O}\) chung
OM=ON (gt)
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét \(\Delta AMN\) và \(\Delta BNM\) có:
AN=BM (cmt)
\(\widehat {NAM} = \widehat {MBN}\) (cmt)
AM=BN (cmt)
=>\(\Delta AMN = \Delta BNM\)(c.g.c)

Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
O y x A B C D I
a, Xét tam giác OAD và tam giác OCB có :
OA = AC (gt)
OD = OB ( gt)
DOB là góc chung
=> tam giác OAD = tam giác OCB ( c . g . c)
b, Xét tam giác OID và tam giác OIB có :
OD = OB (gt)
OI là cạnh chung
ID = IB (gt)
=> tam giác OID = tam giác OIB ( c . c . c )
=> OI Là tia pg xOy