tìm X
x\(\varepsilon\)ƯC(29,30)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
1
C1
2
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
29.
Do \(M\in\Delta\) nên tọa độ có dạng: \(M\left(m;2m+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(m-4;2m+4\right)\\\overrightarrow{BM}=\left(m-5;2m-4\right)\\\overrightarrow{CM}=\left(m-1;2m+2\right)\end{matrix}\right.\)
\(\Rightarrow AM^2+BM^2+CM^2\)
\(=\left(m-4\right)^2+\left(2m+4\right)^2+\left(m-5\right)^2+\left(2m-4\right)^2+\left(m-1\right)^2+\left(2m+2\right)^2\)
\(=15m^2-12m+78\)
\(=15\left(m-\dfrac{2}{5}\right)^2+\dfrac{378}{5}\ge\dfrac{378}{5}\)
Dấu "=" xảy ra khi \(m=\dfrac{2}{5}\Rightarrow M\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
30.
Đặt \(f\left(x\right)=x^2-6x-7\)
Đồ thị hàm \(y=\left|f\left(x\right)\right|=\left|x^2-6x-7\right|\) được tạo ra bằng cách lấy đối xứng phần bên dưới trục Ox của đồ thị \(f\left(x\right)\) lên như hình vẽ:
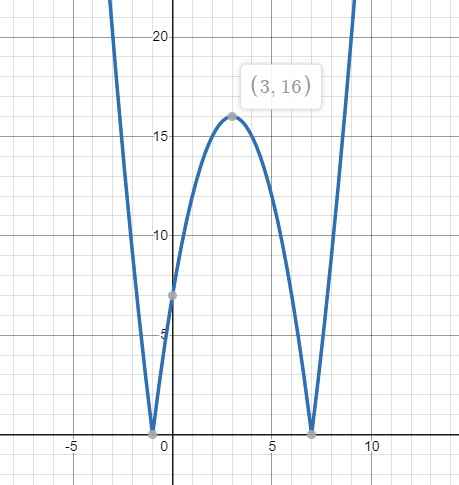
Từ đồ thị ta thấy pt có 4 nghiệm pb khi và chỉ khi: \(0< m< 16\)
\(\Rightarrow\) Có 15 giá trị nguyên của m
TM
2
MC
26 tháng 7 2021
\(ƯC\left(8,12\right)=\left\{\pm1;\pm2;\pm4\right\}\)
\(ƯC\left(12;15;30\right)=\left\{\pm1;\pm3\right\}\)
\(ƯC\left(60;72\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
\(ƯC\left(24;42\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
TM
1
26 tháng 7 2021
a) { 1; 2; 4 }
b) { 1; 3 }
c) { 1; 2; 3; 4; 6; 12 }
d) { 1; 2; 3; 6 }
TM
1
KZ
26 tháng 7 2021
Ý bn là tìm phần tử à:
a, ƯC(8;12)= ƯCLN (8;12)
Ta có: 8= 23 và 12 = 22.3
\(\Rightarrow\)ƯCLN(8;12)= 22= 4
\(\Rightarrow\)ƯC (8;12)= Ư(4)= {1;2;4}
b, ƯC (12;15;30)= ƯCLN (12;15;30)
Ta có: 12= 22.3
15= 3.5
30= 3.2.5
\(\Rightarrow\)ƯCLN (12;15;30)= 2.3= 6
\(\Rightarrow\)ƯC (12;15;30)= Ư(6)= {1;2;3;6}
c, ƯC (60;72)= ƯCLN (60;72)
Ta có: 60= 22.3.5 và 72= 23.32
\(\Rightarrow\)ƯCLN (60;72)= 22= 4
\(\Rightarrow\)ƯC(60;72)= Ư(4)= {1;2;4}
d, ƯC (24;42)= ƯCLN (24;42)
Ta có: 24= 23.3 và 42= 2.3.7
\(\Rightarrow\)ƯCLN (24;42)= 3
\(\Rightarrow\)ƯC (24;42)= Ư(3)= {1;3}
Chúc bn học tốt
H
1
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
9 tháng 11 2019
a, Ta có : \(Ư\left(16\right)=1;2;4;8;16\) và \(Ư\left(24\right)=1;2;3;4;6;8;12;24\)
\(\RightarrowƯC\left(16;24\right)=1;2;4;8\)
b, Ta có : \(\hept{\begin{cases}Ư\left(60\right)=1;2;3;4;5;6;10;12;15;20;20;60\\Ư\left(90\right)=1;2;3;5;6;9;10;15;18;30;45;90\end{cases}}\)
\(\RightarrowƯC\left(60;90\right)=1;2;3;5;6;15;30\)
c, Ta có : \(\hept{\begin{cases}Ư\left(18\right)=1;2;3;6;9;18\\Ư\left(30\right)=1;2;3;5;6;10;15;30\\Ư\left(42\right)=1;2;3;6;7;14;21;42\end{cases}}\)\(\RightarrowƯC\left(18;30;42\right)=1;2;3;6\)
d,Ta có : \(\hept{\begin{cases}Ư\left(26\right)=1;2;13;26\\Ư\left(39\right)=1;3;13;39\\Ư\left(48\right)=1;2;4;6;8;12;16;24;48\end{cases}}\)\(\RightarrowƯC\left(26;39;48\right)=1\)
CT
1
KV
9 tháng 10 2023
1) 12 = 2².3
24 = 2³.3
⇒ ƯCLN(12; 24) = 2².3 = 12
⇒ ƯC(12; 24) = Ư(12) = {1; 2; 3; 4; 6; 12}
2) 15 = 3.5
20 = 2².5
⇒ ƯCLN(15; 20) = 5
⇒ ƯC(15; 20) ={1; 5}
3) 25 = 5²
40 = 2³.5
⇒ ƯCLN(25; 50) = 5
⇒ ƯC(25; 40) = Ư(5) = {1; 5}
4) 30 = 2.3.5
45 = 3².5
⇒ ƯCLN(30; 45) = 3.5 = 15
⇒ ƯC(30; 45) = {1; 3; 5; 15}
NN
0
\(x\in\left\{1;-1\right\}\)
Ư(29)={29}
Ư(30)={2.3.5}
x=rỗng