cho hình chữ nhật ABCD. Điểm M nằm trên đường chéo AC. gọi N là điểm đối xứng của D qua m, kẻ NH vuông góc với AB và NK vuông góc với BC . Chứng minh 3 điểm M,H,K thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Lời giải:
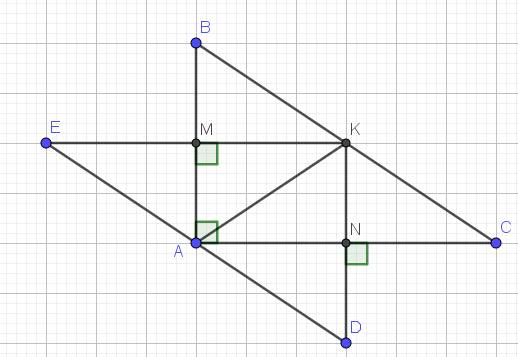
a. Tứ giác $AMKN$ có 3 góc vuông $\widehat{A}=\widehat{M}=\widehat{N}=90^0$ nên $AMKN$ là hình chữ nhật.
b.
Xét tam giác $AEM$ và $AKM$ có:
$MA$ chung
$\widehat{AME}=\widehat{AMK}=90^0$
$EM=KM$ (do $E,K$ đối xứng nhau qua $M$)
$\Rightarrow \triangle AEM=\triangle AKM$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{KAM}(1)$
Tương tự:
$\triangle AKN=\triangle ADN$ (c.g.c)
$\Rightarrow \widehat{DAN}=\widehat{KAN}(2)$
Từ $(1); (2)\Rightarrow \widehat{EAM}+\widehat{MAN}+\widehat{DAN}=\widehat{KAM}+\widehat{MAN}+\widehat{KAN}=2\widehat{MAN}=2.90^0=180^0$
Hay $\widehat{EAD}=180^0$
$\Rightarrow E, A, D$ thẳng hàng.
7 tháng 11 2019
a) ta có : tam giác ABC vuông tại A
=> BAC = 90 độ (1)
có : MD vuông góc AB
=> MDA = 90 độ (2)
Ta có : ME vuông góc AC
=> MEA = 90 độ (3)
Từ (1)(2)(3) => ADME là hình chữ nhật
Gọi O là giao điểm của BN và HC, ta có
\(\widehat{BKN}=\widehat{KBH}=\widehat{BHN}=90^0\)
Suy ra tứ giác BHNK là hình chữ nhật mà O là giao điểm 2 đường chéo nên OB=ON
Mà MD=MN
Suy ra OM//BD(1)
Ta có BHNK là hình chữ nhật\(\Rightarrow\widehat{NHK}=\widehat{NBK}=\widehat{NBC}\)
Mà \(\widehat{NBC}=\widehat{BCA}\)( so le trong)
\(\widehat{BCA}=\widehat{DBC}\)
Suy ra \(\widehat{NHK}=\widehat{DBC}\)
Mà NH//BC (cùng vuông góc với AB)
\(\Rightarrow\)HK//BD(2)
Từ (1),(2) suy ra M,H,K thẳng hàng