\(|x-3|+5-x\) với \(x\ge3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
5 tháng 4 2017
Áp dụng BĐT AM-GM ta có:
\(\left(\frac{12}{5}\right)^x+\left(\frac{15}{4}\right)^x\ge2\sqrt{9^x}=2\cdot3^x\)
\(\left(\frac{15}{4}\right)^x+\left(\frac{20}{3}\right)^x\ge2\sqrt{25^x}=2\cdot5^x\)
\(\left(\frac{20}{3}\right)^x+\left(\frac{12}{5}\right)^x\ge2\sqrt{16^x}=2\cdot4^x\)
Cộng theo vế 3 BĐT trên ta có:
\(2\left[\left(\frac{12}{5}\right)^x+\left(\frac{15}{4}\right)^x+\left(\frac{20}{3}\right)^x\right]\ge2\left(3^x+4^x+5^x\right)\)
\(\Rightarrow\left(\frac{12}{5}\right)^x+\left(\frac{15}{4}\right)^x+\left(\frac{20}{3}\right)^x\ge3^x+4^x+5^x\)
TN
1 tháng 3 2017
Áp dụng BĐT AM-GM ta có:
\(\left(\frac{12}{5}\right)^x+\left(\frac{15}{4}\right)^x\ge2\sqrt{9^x}=2\cdot3^x\)
\(\left(\frac{15}{4}\right)^x+\left(\frac{20}{3}\right)^x\ge2\sqrt{25^x}=2\cdot5^x\)
\(\left(\frac{20}{3}\right)^x+\left(\frac{12}{5}\right)^x\ge2\sqrt{16^x}=2\cdot4^x\)
Cộng theo vế ta có: \(2VT\ge2VP\Leftrightarrow VT\ge VP\)
PN
1
9 tháng 5 2016
Từ bất phương trình ban đầu \(\Leftrightarrow25.5^x-5.5^x>9.3^x-3.3^x\)
\(\Leftrightarrow20.5^x>6.3^x\)
\(\Leftrightarrow\left(\frac{5}{3}\right)^x>\frac{3}{10}\)
\(\Leftrightarrow x>\log_{\frac{5}{3}}\frac{3}{10}\)
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 1:
Vì $a\geq 1$ nên:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}=a+\sqrt{(a-1)^2+4}+\sqrt{a-1}\)
\(\geq 1+\sqrt{4}+0=3\)
Ta có đpcm
Dấu "=" xảy ra khi $a=1$
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 2:
ĐKXĐ: x\geq -3$
Xét hàm:
\(f(x)=x(x^2-3x+3)+\sqrt{x+3}-3\)
\(f'(x)=3x^2-6x+3+\frac{1}{2\sqrt{x+3}}=3(x-1)^2+\frac{1}{2\sqrt{x+3}}>0, \forall x\geq -3\)
Do đó $f(x)$ đồng biến trên TXĐ
\(\Rightarrow f(x)=0\) có nghiệm duy nhất
Dễ thấy pt có nghiệm $x=1$ nên đây chính là nghiệm duy nhất.
10 tháng 10 2018
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}=\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}=\sqrt{\left(\sqrt{x-3}-1\right)^2}+\sqrt{x-3}=\left|\sqrt{x-3}-1\right|+\sqrt{x-3}\)
Nếu \(3\le x< 4\) thì \(\left|\sqrt{x-3}-1\right|+\sqrt{x-3}=1-\sqrt{x-3}+\sqrt{x-3}=1\)
Nếu \(x\ge4\) thì \(\left|\sqrt{x-3}-1\right|+\sqrt{x-3}=\sqrt{x-3}-1+\sqrt{x-3}=2\sqrt{x-3}-1\)
KK
10 tháng 10 2018
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}\)
=\(\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}\)
=\(\sqrt{\left(x-3+1\right)^2}+\sqrt{x-3}\)
=|x-3+1|+\(\sqrt{x-3}\)
= x-2 + \(\sqrt{x-3}\)
LT
10 tháng 10 2018
\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x-3}\)
\(=\sqrt{x-3+2\sqrt{x-3}+1}+\sqrt{x-3}\)
\(=\sqrt{\left(\sqrt{x-3}+1\right)^2}+\sqrt{x-3}=2\sqrt{x-3}+1\)
N
1
21 tháng 8 2015
Ta có \(x^2-2x+5=\left(x-1\right)^2+4\ge4\to\sqrt{x^2-2x+5}\ge2.\)
\(x^2-2x+2=\left(x-1\right)^2+1\ge1\to\sqrt{x^2-2x+2}\ge1.\)
Vậy vế trái \(\ge2+1=3.\)
8 tháng 3 2022
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
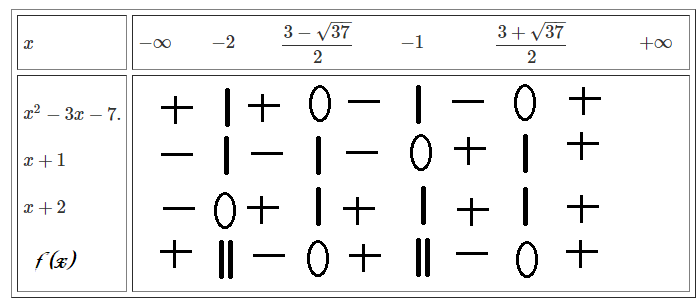
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
PT
2
13 tháng 2 2020
Mình nghĩ là thế này
Ta có: x2+1>0 ∀xϵR
x2+2x+3=(x+1)2+1>0 ∀xϵR
x2+4x+5=(x+2)2+1 >0 ∀xϵR
nên \(\sqrt{x^2+1}+2\sqrt{x^2+2x+3}\ge3\sqrt{x^2+4x+5}\)
\(\Leftrightarrow\sqrt{x^2+1}+2\sqrt{\left(x+1\right)^2+1}\ge3\sqrt{\left(x+2\right)^2+1}\)
\(\Leftrightarrow x+1+2\left(x+1\right)+2\ge3\left(x+2\right)+3\)
\(\Leftrightarrow x+3+2x+2\ge3x+6+3\)
\(\Leftrightarrow3x+5\ge3x+9\Leftrightarrow0x\ge4\) (vô nghiệm)
Vậy S=∅
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 2 2020
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+1}=a>0\\\sqrt{x^2+2x+3}=b>0\end{matrix}\right.\)
\(a+2b\ge3\sqrt{2b^2-a^2}\)
\(\Leftrightarrow a^2+4b^2+4ab\ge18b^2-9a^2\)
\(\Leftrightarrow5a^2+2ab-7b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(5a+7b\right)\ge0\)
\(\Leftrightarrow a-b\ge0\) (do \(5a+7b>0\))
\(\Leftrightarrow a\ge b\Leftrightarrow\sqrt{x^2+1}\ge\sqrt{x^2+2x+3}\)
\(\Leftrightarrow x^2+1\ge x^2+2x+3\Leftrightarrow x\le-1\)
Vậy nghiệm của BPT là \(x\le-1\)
|x−3|+5−x với x≥3