Cho đường tròn (O,R) đường kính AB. Vẽ tiếp tuyến Bx của(O'). Trên cùng nửa mặt phẳng bờ AB có chứa Bx . Lấy M ϵ (O) ( M khác A,B) sao cho MA> MB. Tia MA cắt Bx tại C. Từ C kẻ tiếp tuyến CD với (O) .D là tiếp điểm.
c, Chứng minh OC ⊥ BD
b, chứng minh O, C, B,D cùng thuộc 1 đường tròn.
c, Chứng minh CMD= CDA
d, Kẻ MH ⊥ AB tại H. tìm vị trí của M để chu vi tam giác OMH max

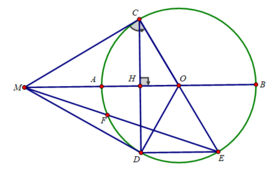
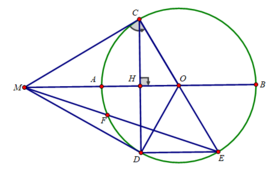
Bạn tụ vẽ hình nha
a, Theo tính chất 2 tiếp tuyến cắt nhau, ta có: CB = CD
mà OB = OD = R
⇒ BD là đường trung trực của OC
⇒ OC ⊥ BD (đpcm)
b, Gọi I là trung điểm của OC thì:
ΔOBC vuông tại B có BI là trung tuyến ứng với cạnh huyền
⇒ BI = IO = IC
ΔODC vuông tại D có DI là trung tuyến ứng với cạnh huyền
⇒ DI = IO = IC
⇒BI = DI = IO = IC
⇒ 4 điểm O,B,C,D cùng thuộc một đường tròn
c,\(\widehat{DMC}\) là góc ngoài tại M của Δ DAM
\(\Rightarrow\widehat{DMC}=\widehat{ADM}+\widehat{DAM}\)
Mà \(\widehat{DAM}=\widehat{MDC}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau)
\(\Rightarrow\widehat{ADM}+\widehat{DAM}=\widehat{ADM}+\widehat{MDC}\)
\(\Rightarrow\widehat{DMC}=\widehat{CDA}\)