\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+1}\)=\(\dfrac{z}{x+y-2}\)=x+y+z giúp mik vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)
\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)
\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1
⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)
Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1
3\(x\) = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)
\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)
Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2
3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)
Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)
\(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)
Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))
16 tháng 8 2023
TH1: x + y + z ≠≠ 0
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
xy+z+1��+�+1 = yx+z+2��+�+2 = zx+y−3��+�−3 = x+y+zy+z+1+x+z+2+x+y−3�+�+��+�+1+�+�+2+�+�−3
= x+y+zx+y+z+x+y+z�+�+��+�+�+�+�+� = x+y+z2(x+y+z)�+�+�2(�+�+�) = 1212
⇒ x + y + z = 1212
⇒ x + y = 1212 - z
x + z = 1212 - y
y + z = 1212 - x
Thay y + z + 1 = 1212 - x + 1
⇒ x12−x+1�12−�+1 = 1212
⇒ 2x = 1212 - x + 1
⇒ 2x + x = 1212 + 1
⇒ 3x = 3232
⇒ x = 1212
Thay x + z + 2 = 1212 - y + 2
⇒ y12−y+2�12−�+2 = 1212
⇒ 2y = 1212 - y + 2
⇒ 2y + y = 1212 + 2
⇒ 3y = 5252
⇒ y = 5656
Thay x + y - 3 = 1212 - z - 3
⇒ z12−z−3=�12−�−3=\frac{1}{2}$
⇒ 2z = 1212 - z - 3
⇒ 2z + z = 1212 - 3
⇒ 3z = −52−52
⇒ z = −56−56
TH2: x + y + z = 0
⇒ xy+z+1��+�+1 = yx+z+2��+�+2 = zx+y−3��+�−3 = 0
⇒ x = y = z = 0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
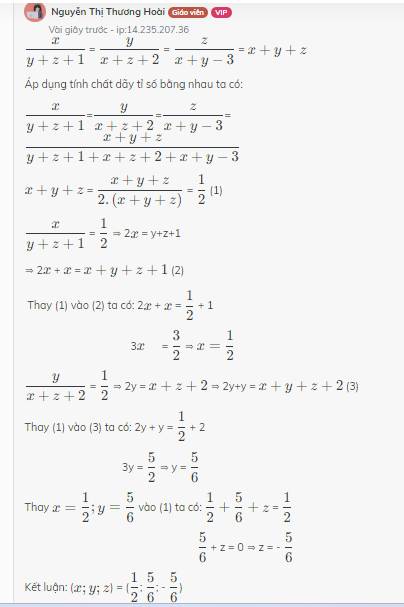
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934
17 tháng 12 2021
x+y+z=0
nên x+y=-z; y+z=-x; x+z=-y
\(\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\)
\(=\dfrac{x+y}{y}\cdot\dfrac{y+z}{z}\cdot\dfrac{x+z}{x}=-1\)
MH
7 tháng 2 2022
\(\dfrac{1}{\left(x-y\right)\left(y-z\right)}+\dfrac{1}{\left(y-z\right)\left(z-x\right)}+\dfrac{1}{\left(z-x\right)\left(x-y\right)}\)(đk: \(x\ne y\ne z\))
\(=\dfrac{z-x+x-y+y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=\dfrac{0}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=0\)
7 tháng 2 2022
Chắc đề là tính ha!
\(=\dfrac{x+y+y-z+x-y}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\\ =\dfrac{0}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\\ =0\\ Vậy.A=0\)
LL
1 tháng 3 2018
a) Với \(x+y+z=0\) ta tìm được \(\left(x;y;z\right)\rightarrow\left(0;0;0\right)\)
Với \(x+y+z\ne0\) áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}\)
Hay: \(x+y+z=\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}y+z=\dfrac{1}{2}-x\\x+z=\dfrac{1}{2}-y\\x+y=\dfrac{1}{2}-z\end{matrix}\right.\)
Thay vào đề bài ta được:
\(\dfrac{x}{\dfrac{1}{2}-x+1}=\dfrac{y}{\dfrac{1}{2}-y+1}=\dfrac{z}{\dfrac{1}{2}-z-2}=\dfrac{1}{2}\) Dễ dàng tìm được x;y;z
b) Theo đề bài ta có sẵn x+y+z khác 0
Áp dụng dãy tỉ số rồi làm tương tự câu a
Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{x+z+1}=\dfrac{x}{x+y-2}=\dfrac{x+y+z}{y+z+1+x+z+1+x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{y+z+1}=\dfrac{1}{2}\left(1\right)\\\dfrac{y}{x+z+1}=\dfrac{1}{2}\left(2\right)\\x+y+z=\dfrac{1}{2}\left(3\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow2x=y+z+1\)
\(\Rightarrow2x=\dfrac{1}{2}-x+1\left(do.\left(3\right)\right)\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(\left(2\right)\Rightarrow2y=x+z+1\)
\(\Rightarrow2y=\dfrac{1}{2}-y+1\left(do.\left(3\right)\right)\)
\(\Rightarrow y=\dfrac{1}{2}\)
\(\left(3\right)\Rightarrow z=\dfrac{1}{2}-x-y=\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{2}=-\dfrac{1}{2}\)
Vậy \(\left(x;y;z\right)\in\left\{\dfrac{1}{2};\dfrac{1}{2};-\dfrac{1}{2}\right\}\)