Giúp em bài 14 15 16 với ạ😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử đường thẳng chắn trên hai trục tọa độ 2 đoạn bằng nhau bằng a \(\left(a\ne0\right)\)
Khi đó, tọa độ giao điểm là: (a;0), (0;a)
Phương trình đường thẳng là: \(\dfrac{x-a}{a-0}=\dfrac{y-0}{0-a}\Leftrightarrow-a\left(x-a\right)=ay\)
\(\Leftrightarrow-x+a=y\) (*)
a. Thay M(-4;10) vào (*) ta được: \(-\left(-4\right)+a=10\Rightarrow a=6\)
Phương trình đường thẳng cần tìm là: y=-x+6
b. Thay M(2;1) vào (*) ta được: \(-2+a=1\Rightarrow a=3\)
Phương trình đường thẳng cần tìm là: y=-x+3

5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP


11:
a: \(BD=AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
|vecto AB+vecto AD|
=|vecto AB+vecto BC|
=|vecto AC|
=5a
b: Gọi M là trung điểm của BC
=>BM=CM=BC/2=2a
\(AM=\sqrt{AB^2+BM^2}=a\sqrt{13}\)
Xét ΔABC có AM là trung tuyến
nên vecto AB+vecto AC=2*vecto AM
=>|vecto AB+vecto AC|=2|vecto AM|
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)

10:
a: A=(2^2-1)(2^2+1)*...*(2^16+1)
=(2^4-1)(2^4+1)(2^8+1)(2^16+1)
=(2^8-1)(2^8+1)(2^16+1)
=(2^16-1)(2^16+1)
=2^32-1
b: B=(127+73)^2=200^2=40000
c: C=18^8-18^8+1=1
d: D=560*1000/200^2=14

tk
Mid_Autumn festival is one of the popular celebrations in the Viet Nam.Every year,it's on the 15th day of the 8th lunar month. It's organized so that people celebrate the largest full moon in the year.
In that festival, children wear masks, parade on the street have parties with special cakes and lots of fruits.
I feel happy when taking part in it because it makes me exited and helps me remember about my childish.

Bài 1:
Kiểu hình ở F2: 75% Hạt vàng : 25% Hạt xanh.
Biện luận: Lai cây hạt vàng với cây hạt xanh cho đời con F1 toàn cây hạt vàng, suy ra tính trạng hạt vàng trội hơn so với hạt xanh. Do P thuần chủng nên cây hạt vàng và cây hạt xanh ở P đều mang kiểu gen đồng hợp.
Quy ước gen: Alen A quy định tính trạng hạt vàng trội hoàn toàn so với alen a quy định tính trạng hạt xanh.
Sơ đồ lai:
PTC: AA (Hạt vàng) x aa (Hạt xanh)
G: (A)_(a)
F1: 100% Aa (Hạt vàng)
F1xF1: Aa (Hạt vàng) x Aa (Hạt vàng)
G: (A,a)_(A,a)
F2: 1AA : 2Aa : 1aa (3 Hạt vàng : 1 Hạt xanh)
Bài 2:
Kiểu hình ở F2: 75% Hạt trơn : 25% Hạt nhăn.
Bài 3:
Kiểu hình ở F2: 56,25% Hạt vàng, trơn : 18,75% Hạt vàng, nhăn : 18,75% Hạt xanh, trơn : 6,25% Hạt xanh, nhăn.

\(\dfrac{3}{1-\sqrt{2}}+\dfrac{\sqrt{2}-1}{\sqrt{2}+1}=\dfrac{3\left(\sqrt{2}+1\right)-\left(\sqrt{2}-1\right)^2}{-1}=-\left(3\sqrt{2}+3-3+2\sqrt{2}\right)=-5\sqrt{2}\)
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}+\dfrac{6}{1-\sqrt{5}}=\dfrac{\left(\sqrt{5}-1\right).\left(1-\sqrt{5}\right)+6.\left(\sqrt{5}+1\right)}{-4}=\dfrac{6-2\sqrt{5}-6\sqrt{5}-6}{4}=\dfrac{-8\sqrt{5}}{4}=-2\sqrt{5}\)
\(\dfrac{\sqrt{2}-\sqrt{3}}{2-\sqrt{6}}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}+2}=\dfrac{\left(\sqrt{2}-\sqrt{3}\right).\left(\sqrt{6}+2\right)+\left(\sqrt{3}-\sqrt{2}\right).\left(2-\sqrt{6}\right)}{-2}=\dfrac{2\left(\sqrt{12}-\sqrt{18}\right)}{-2}=\sqrt{18}-\sqrt{12}\)
\(\dfrac{-31+8\sqrt{x}-x}{x-8\sqrt{x}+15}-\dfrac{\sqrt{x}+5}{\sqrt{x}-3}-\dfrac{3\sqrt{x}-1}{5-\sqrt{x}}\)
\(=\dfrac{-31+8\sqrt{x}-x}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+5}{\sqrt{x}-3}+\dfrac{3\sqrt{x}-1}{\sqrt{x}-5}\)
\(=\dfrac{-31+8\sqrt{x}-x-x+25+3x-9\sqrt{x}-\sqrt{x}+3}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)


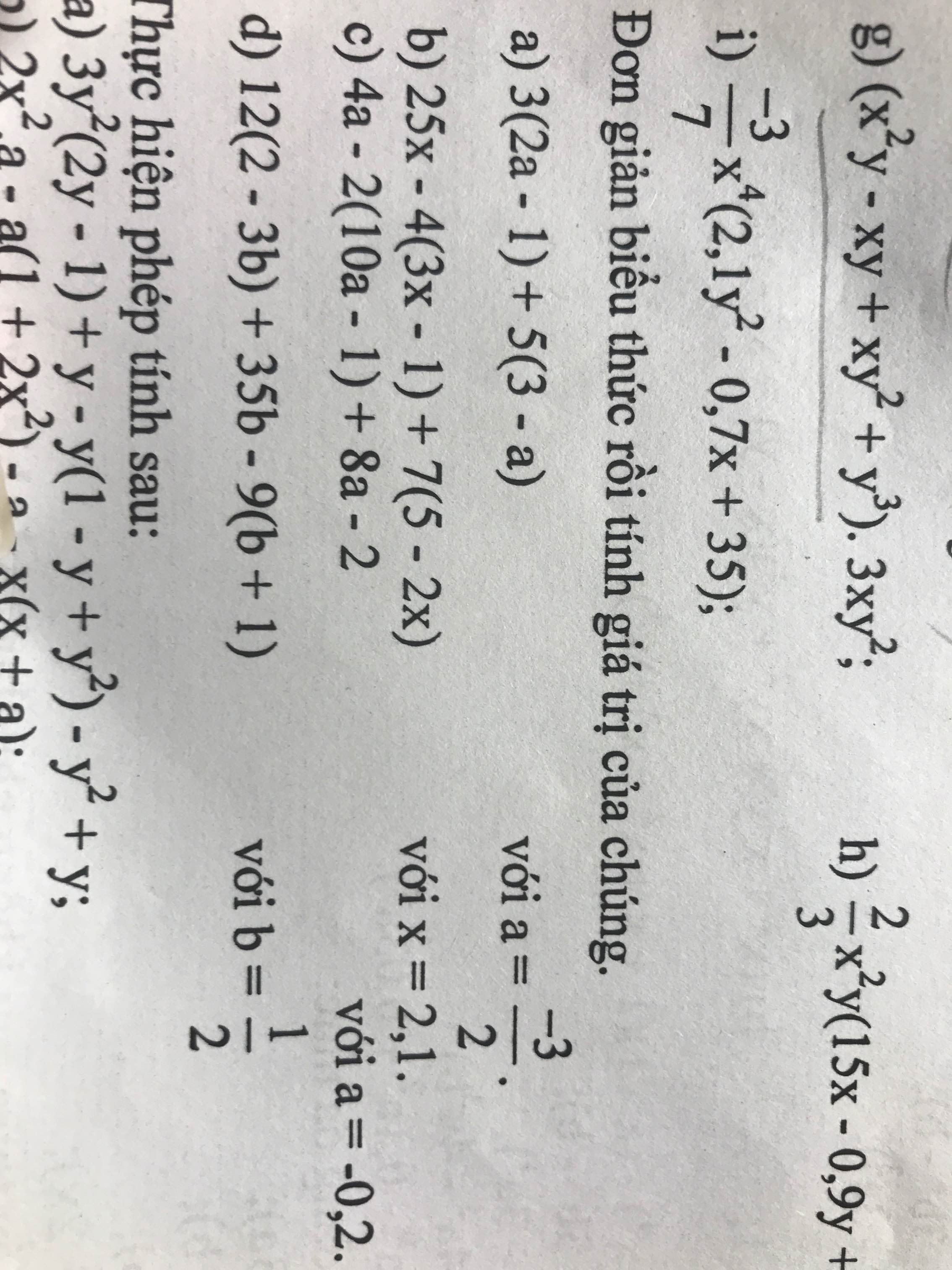





 giải giúp em bài 14 15 16 17 của bài 14 nha
giải giúp em bài 14 15 16 17 của bài 14 nha