Hai chi đội thiếu niên, có 42 đội viên ở chi đội Vừ A Dính và 54 đội viên ở chi đội Lê Văn Tám, khi sinh hoạt anh tổng phụ trách muốn chia thành nhiều tổ. Hỏi có thể chia thành nhiều nhất là mấy tổ để số đội viên của hai chi đội được chia đều vào các tổ ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
gọi x là số nhóm nhiều nhất có thể chia và là ƯCLN ( 36; 48)
36= 22 . 33
48= 24 . 3
có thể chia nhiều nhất thành số nhóm là:
22 . 3 = 12 ( nhóm )
Khi đó mỗi nhóm có số bạn nam là: 36 : 12 = 3 bạn
Khi đó mỗi nhóm có số bạn nữ là: 48 : 12 = 4 bạn
Vậy có thể chia thành nhiều nhất 12 nhóm và mỗi nhóm có 3 bạn nam, 4 bạn nũ
MH
9 tháng 3 2016
Ta lập luận để có các kết luận sau:
- Tổng số Đội viên phải là số chia hết cho 3.
- Tổng số Đội viên là 42, 45 hoặc 48
- Sau lần chuyển thứ 3, số đội viên đội A là số chẵn
- Sau lần chuyển thứ 2, số đội viên đội C là số chẵn
Ta xét 3 trường hợp sau:
a, TH1: Tổng số Đội viên là 42.
Sau lần chuyển thứ 3, mỗi đội có: 42 : 3 = 14 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 14 : 2 = 7 (bạn) và đội C có 14 + 7 = 21 (bạn)
Số đội viên của đội C không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 42
b, TH2: Tổng số Đội viên là 45.
Sau lần chuyển thứ 3, mỗi đội có: 45 : 3 = 15 (bạn)
Số đội viên của đội A không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 45
c, TH3: Tổng số Đội viên là 48.
Sau lần chuyển thứ 3, mỗi đội có: 48 : 3 = 16 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 16 : 2 = 8 (bạn) và đội C có 16 + 8 = 24 (bạn)
Vậy sau lần chuyển thứ nhất, đội C có: 24 : 2 = 12 (bạn) còn đội B có: 16 + 12 = 28 (bạn)
Do đó: Lúc đầu số lượng đội viên như sau:
- Đội B: 28 : 2 = 14 (bạn)
- Đội A: 14 + 8 = 22 (bạn)
- Đội C: 12 (bạn)
Nguồn: Câu lạc bộ Toán Tiểu học Lộc Hà, Hà Tĩnh.
LN
9 tháng 3 2016
Ta lập luận để có các kết luận sau:
- Tổng số Đội viên phải là số chia hết cho 3.
- Tổng số Đội viên là 42, 45 hoặc 48
- Sau lần chuyển thứ 3, số đội viên đội A là số chẵn
- Sau lần chuyển thứ 2, số đội viên đội C là số chẵn
Ta xét 3 trường hợp sau:
a, TH1: Tổng số Đội viên là 42.
Sau lần chuyển thứ 3, mỗi đội có: 42 : 3 = 14 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 14 : 2 = 7 (bạn) và đội C có 14 + 7 = 21 (bạn)
Số đội viên của đội C không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 42
b, TH2: Tổng số Đội viên là 45.
Sau lần chuyển thứ 3, mỗi đội có: 45 : 3 = 15 (bạn)
Số đội viên của đội A không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 45
c, TH3: Tổng số Đội viên là 48.
Sau lần chuyển thứ 3, mỗi đội có: 48 : 3 = 16 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 16 : 2 = 8 (bạn) và đội C có 16 + 8 = 24 (bạn)
Vậy sau lần chuyển thứ nhất, đội C có: 24 : 2 = 12 (bạn) còn đội B có: 16 + 12 = 28 (bạn)
Do đó: Lúc đầu số lượng đội viên như sau:
- Đội B: 28 : 2 = 14 (bạn)
- Đội A: 14 + 8 = 22 (bạn)
- Đội C: 12 (bạn)
Ai tích mình mình tích lại cho
17 tháng 9 2016
Ta lập luận để có các kết luận sau:
- Tổng số Đội viên phải là số chia hết cho 3.
- Tổng số Đội viên là 42, 45 hoặc 48
- Sau lần chuyển thứ 3, số đội viên đội A là số chẵn
- Sau lần chuyển thứ 2, số đội viên đội C là số chẵn
Ta xét 3 trường hợp sau:
a, TH1: Tổng số Đội viên là 42.
Sau lần chuyển thứ 3, mỗi đội có: 42 : 3 = 14 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 14 : 2 = 7 (bạn) và đội C có 14 + 7 = 21 (bạn)
Số đội viên của đội C không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 42
b, TH2: Tổng số Đội viên là 45.
Sau lần chuyển thứ 3, mỗi đội có: 45 : 3 = 15 (bạn)
Số đội viên của đội A không phải là số chẵn
Vậy số đội viên của cả 3 đội không thể là 45
c, TH3: Tổng số Đội viên là 48.
Sau lần chuyển thứ 3, mỗi đội có: 48 : 3 = 16 (bạn)
Suy ra, sau lần chuyển thứ hai đội A có 16 : 2 = 8 (bạn) và đội C có 16 + 8 = 24 (bạn)
Vậy sau lần chuyển thứ nhất, đội C có: 24 : 2 = 12 (bạn) còn đội B có: 16 + 12 = 28 (bạn)
Do đó: Lúc đầu số lượng đội viên như sau:
- Đội B: 28 : 2 = 14 (bạn)
- Đội A: 14 + 8 = 22 (bạn)
- Đội C: 12 (bạn)
MH
14 tháng 12 2015
a. Gọi số em xếp đc nhiều nhất là x.
Ta có: 147, 168, 189 chia hết cho x; x lớn nhất
=> x = ƯCLN(147, 168, 189)
147 = 3.72; 168=23.3.7; 189=33.7
=> x = ƯCLN(147, 168, 189) = 3.7=21
Vậy mỗi hàng nhiều nhất 21 em.
b. Lúc đó:
Đôi 1 có: 147:21=7 (em)
Đội 2 có: 168:21=8 (em)
Đội 3 có: 189:21=9 (em).
28 tháng 5 2015
Gọi x là số thiếu nhi nhiều nhất trong mỗi hàng.
Suy ra x = ƯCLN ( 147,168,189).
147 = 3.72
168 = 23.3.7
189 = 33.7
ƯCLN (147,168,189) = 3.7 = 21.
Vậy mỗi hàng có nhiều nhất 21 em.
Số hàng trong đội thứ nhất là : 147:21 = 7 (em)
Số hàng trong đội thứ hai là : 168:21 = 8 (em)
Số hàng trong đội thứ ba là: 189:21 = 9 (em)
28 tháng 5 2015
đội 1
mỗi hàng có 49 em, dc 3 hàng
đội 2
mỗi hàng có 56 em, dc 3 hàng
đội 3
mỗi hàng có 63 em, dc 3 hàng
kết quả như thế bạn có thể suy từ từ cách giải và lời giải
CM
19 tháng 3 2018
Chọn A
Gọi A là biến cố “Đội tuyển Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng”.
Ta có: 
.
Do đó: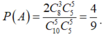 
.
10 tháng 12 2016
gọi a là số đội chơi cần tìm(a>0,a thuộc N)
ta có 24 chia hết a
18 chia hết a ( suy ra từ 2 cái ) a thuộc ƯCLN (24,18)
ta thấy 24=\(2^3.3\) 18=\(2.3^2\)
suy ra ƯCLN(24,18)=2.3=6
suy ra chia đc nhiều nhất 6 đội
9 tháng 8 2016
mình lười giải lĩ nên chỉ giải thích thôi nhé bạn không hiểu thì nhắn tin hỏi mình
9 tháng 8 2016
Bài đầu :
Bạn tìm BCNN của 30, 40, 36 sau đó nhân với 2 được bao nhiêu lấy số đó trừ đi 10 là ra.
Bài tiếp cũng dạng đó nhưng khác tí