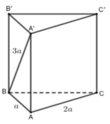
Cho khối lăng trụ ABC.A'B'C', khoảng cách từ C đến đường thẳng BB' bằng \(2\), khoảng cách từ A đến các đường thẳng BB' và CC' lần lượt bằng \(1\) và \(\sqrt{3}\). Hình chiếu vuông góc của A lên mặt phẳng (A'B'C') là trọng tâm G' của tam giác A'B'C' và A'G' = \(\dfrac{4}{3}\). Thể tích của khối lăng trụ đã cho bằng
A. \(\dfrac{8}{3}\)
B. \(2\)
C. \(\dfrac{2}{3}\)
D. \(\dfrac{4}{3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
28 tháng 4 2017
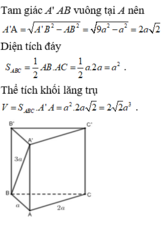
Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:

CM
3 tháng 6 2019
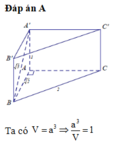
Chọn C
Gọi h là độ dài cạnh bên của lăng trụ đứng đã cho.
Vì MNPQ là tứ diện đều nên
![]()
![]()
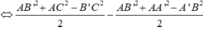 = 0
= 0
![]()
![]()
![]()
*Chú ý một khối tứ diện đều (tất cả các cạnh bằng nhau) hoặc một khối tứ diện gần đều (độ dài cặp cạnh đối bằng nhau) thì cặp cạnh đối của chúng vuông góc với nhau (xem chương góc và khoảng cách).
*Chú ý tích vô hướng cho hai véctơ cùng gốc
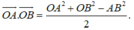
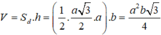
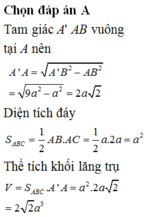




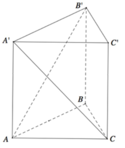
Chọn B