22x+1+4x=48
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3) \(...\Rightarrow2^x\left(2^3+1\right)=36\)
\(\Rightarrow2^x.9=36\)
\(\Rightarrow2^x=4\)
\(\Rightarrow2^x=2^2\Rightarrow x=2\)
4) \(...\Rightarrow4^{x+1}-4^x=12\)
\(\Rightarrow4^x\left(4-1\right)=12\)
\(\Rightarrow4^x.3=12\)
\(\Rightarrow4^x=4=4^1\Rightarrow x=1\)
5) \(...\Rightarrow5^{x+1}\left(5^2-1\right)=3000\)
\(\Rightarrow5^{x+1}.24=3000\)
\(\Rightarrow5^{x+1}=125\)
\(\Rightarrow5^{x+1}=5^3\)
\(\Rightarrow x+1=3\)
\(\Rightarrow x=2\)
6) Bạn xem lại đề
a. \(2^x.2^3+2^x=36\)
\(2^x\left(2^3+1\right)=36\)
\(2^x.9=36\)
\(2^x=4\Rightarrow x=2\)
b. \(4^x.4^1-\left(2^2\right)^x=12\)
\(4^x.4-4^x=12\)
\(4^x\left(4-1\right)=12\)
\(4^x.3=12\)
\(4^x=4\)
x = 1
c. \(5^x.5^3-5^x.5^1=3000\)
\(5^x\left(5^3-5^1\right)=3000\)
\(5^x.120=3000\)
\(5^x=25\)
x = 2
d. \(4^{x+1}=2^{2x}\)
\(4^x.4=\left(2^2\right)^x\)
\(4^x.4=4^x\)
Có vẻ như câu 4 này để bài thiếu


\(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-\frac{1}{2}\left(2sinx.cosx\right)^2=1-\frac{1}{2}sin^22x\)

\(\frac{sin^22x-4sin^2x}{sin^22x+4sin^2x-4}=\frac{4sin^2x.cos^2x-4sin^2x}{4sin^2x.cos^2x+4\left(sin^2x-1\right)}\)
\(=\frac{4sin^2x\left(cos^2x-1\right)}{4sin^2x.cos^2x-4cos^2x}=\frac{-4sin^4x}{4cos^2x\left(sin^2x-1\right)}=\frac{sin^4x}{cos^4x}=tan^4x\)

Điều kiện của phương trình là m > 1/2
Với điều kiện đó vế trái dương, nên vế phải cũng dương nên m > 1. Lúc đó ta có:
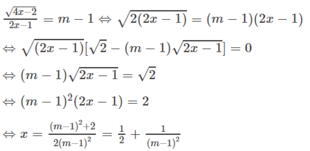
Giá trị ![]() thỏa mãn điều kiện x > 1/2
thỏa mãn điều kiện x > 1/2
Kết luận. Với m ≤ 1 phương trình vô nghiệm.
Với m > 1 nghiệm của phương trình là
![]()

\(\frac{sin^22x+4sin^2x-4}{1-8sin^2x-cos4x}=\frac{4sin^2x.cos^2x-4\left(1-sin^2x\right)}{1-8sin^2x-\left(1-2sin^22x\right)}=\frac{4sin^2x.cos^2x-4cos^2x}{2sin^22x-8sin^2x}\)
\(=\frac{-4cos^2x\left(1-sin^2x\right)}{8sin^2x.cos^2x-8sin^2x}=\frac{-4cos^2x.cos^2x}{-8sin^2x\left(1-cos^2x\right)}=\frac{cos^4x}{2sin^4x}=\frac{1}{2}cot^4x\)
\(\frac{cos2x}{cot^2x-tan^2x}=\frac{cos2x.sin^2x.cos^2x}{cos^4x-sin^4x}=\frac{\left(cos^2x-sin^2x\right).\left(2sinx.cosx\right)^2}{4\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)}=\frac{1}{4}sin^22x\)
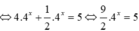
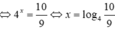
\(2^{2x+1}+4^x=48\)
\(\Leftrightarrow2^{2x+1}+2^{2x}=48\)
\(\Leftrightarrow2^{2x}\left(2+1\right)=48\)
\(\Leftrightarrow2^{2x}=16\)'
\(\Leftrightarrow2^{2x}=2^4\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
\(2^{2x+1}+4^x=48\)
\(\Rightarrow2^{2x+1}+2^{2x}=48\)
\(\Rightarrow2^{2x}.\left(2+1\right)=48\)
\(\Rightarrow2^{2x}.3=48\)
\(\Rightarrow2^{2x}=16\)
\(\Rightarrow2^{2x}=2^4\)
\(\Rightarrow2x=4\)
\(\Rightarrow x=2\)