Cho hàm số y=(2m+1)x. Xác định m để đồ thị hàm số đi qua điểm A(-1;1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
21 tháng 12 2022
a) Điều kiện: m khác -1
Thay tọa độ điểm M(1; -2) vào hàm số, ta có:
(m + 1).1 - 2m = -2
m + 1 - 2m = -2
-m = -2 - 1
-m = -3
m = 3 (nhận)
Vậy m = 3 thì đồ thị hàm số đi qua M(1; -2)
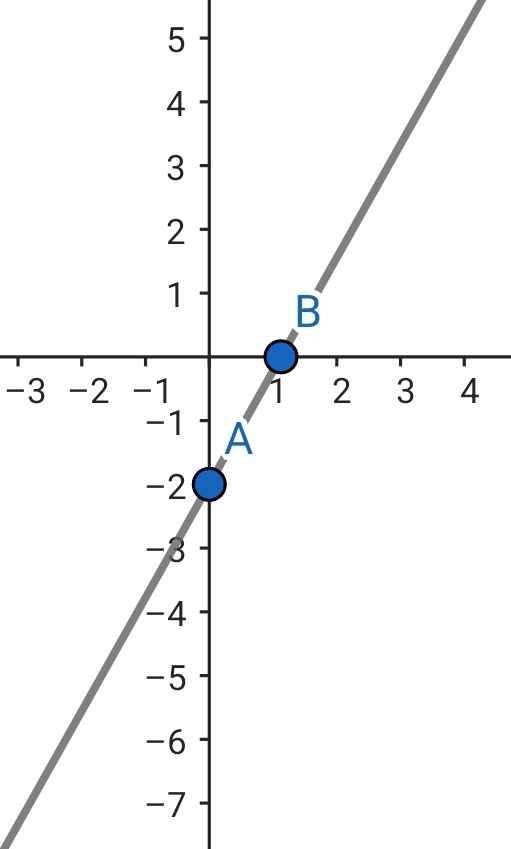
b) Khi m = 1, ta có hàm số:
y = 2x - 2
x = 0 ⇒ y = -2 ⇒A(0; -2)
x = 1⇒y = 0 ⇒B(1; 0)
Đồ thị
CM
5 tháng 6 2018
Thay tọa độ A: x = -1; y = 1 vào y = (2m+1)x ta được
1 = (2m+1).(−1) ⇒ 2m+1= −1
⇒ 2m = −2 ⇒ m = −1
Vậy m = -1
Đáp án cần chọn là: B
30 tháng 7 2023
a: Thay x=-1 và y=1 vào (d), ta được:
-(2m+1)=1
=>2m+1=-1
=>2m=-2
=>m=-1
b: y=(-2+1)x=-x
G
19 tháng 1 2016
Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
- a = 1 > 0 hàm số đồng biến trên R.
bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ |
| +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)
L
11 tháng 1 2020
a) Đths \(y=\left(2m+1\right)x\) đi qua \(A\left(-1;1\right)\)
Ta có:
\(y=\left(2m+1\right)x\)
\(\Rightarrow\left(2m+1\right)\left(-1\right)=1\)
\(\Rightarrow2m+1=-1\)
\(\Rightarrow2m=-2\)
\(\Rightarrow m=-1\)
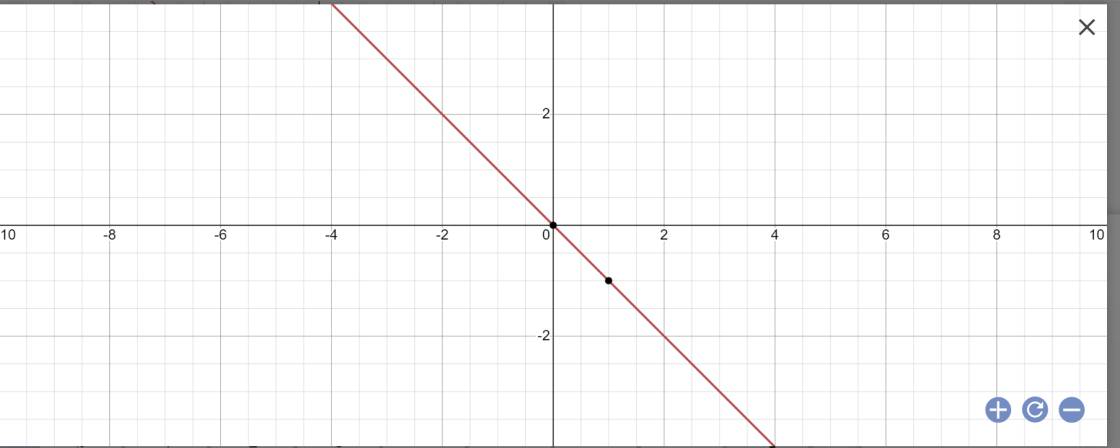
b) Thay \(m=-1\)
\(\Rightarrow y=\left(-2+1\right)x\)
\(\Rightarrow y=-x\)
Lập bảng giá trị:
| \(x\) | \(0\) | \(-2\) |
| \(y=-x\) | \(0\) | \(2\) |
Để A(-1;1) thuộc đồ thị hàm số y=(2m+1)x<=>(2m+1)(-1)=1=>2m+1=-1=>2m=-2=>m=-1