Hệ số góc của đường thẳng: y=-4x+9 là:
A. 4 B.-4x C.-4 D. 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
1
DN
1
TK
16 tháng 5 2021
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
20 tháng 10 2021
2: Vì (d)//(d') nên a=5
Vậy: (d): y=5x+b
Thay x=-2 và y=4 vào (d), ta được:
b-10=4
hay b=14
CM
26 tháng 8 2017
Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k
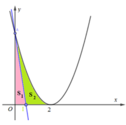
Vì d chia (H) thành 2 phần có diện tích bằng nhau
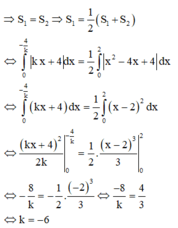
Đáp án A
CM
30 tháng 12 2019
Đáp án A
Phương pháp: Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức :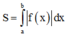 
Cách giải: Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k
Cho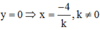 
. Vậy, d cắt Ox tại điểm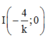 
Giao điểm của y = x 2 - 4 x + 4 và trục hoành: Cho y = 0 => x = 2
=>Để d chia (H) thành 2 phần thì 
Vì d chia (H) thành 2 phần có diện tích bằng nhau
28 tháng 8 2021
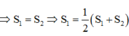
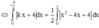
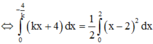
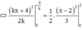
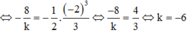
Vì đồ thị hàm số y=ax+b vuông góc với y=-4x+9 nên ta có: -4a=-1
hay \(a=\dfrac{1}{4}\)
chọn C -4