Cho hunhf vuông ABCD. Lấy M thuộc AB. Gọi I,N lần lượt là trung điểm của AB, DM, Lấy E thuộc BC Sao cho BE=BM. Chứng minh AE vuông góc với NI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 1
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1
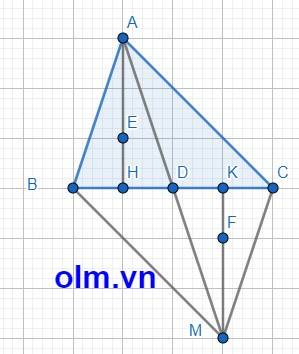
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
K
7 tháng 1
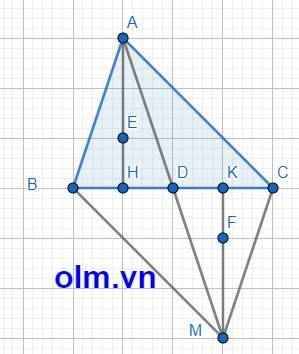
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .