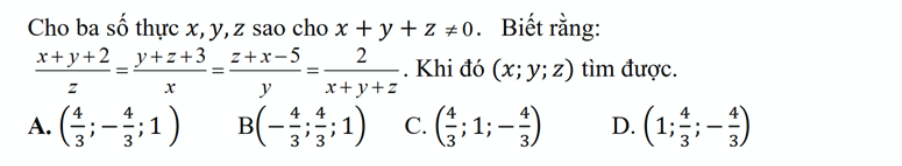Bạn nào giúp mình câu này nhe
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
3
AT
4 tháng 6 2021
\(A=\dfrac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=2\sqrt{y}\)
\(B=\dfrac{x+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}-\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=0\)
AT
4 tháng 6 2021
\(C=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}+\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{x}\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}=\sqrt{x}+\sqrt{y}+\sqrt{x}+\sqrt{y}\)
\(=2\left(\sqrt{x}+\sqrt{y}\right)\)
\(D=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-4\sqrt{xy}}{\sqrt{x}-\sqrt{y}}+\dfrac{y\sqrt{x}-x\sqrt{y}}{\sqrt{xy}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{y}-\sqrt{x}\right)}{\sqrt{xy}}=\sqrt{x}-\sqrt{y}+\sqrt{y}-\sqrt{x}=0\)
A
20 tháng 12 2016
Mục đích học tập của học sinh là :
- Học tập để trở thành con ngoan , trò giỏi , cháu ngoan Bác Hồ , người công dân tốt
- Trở thành con người chân chính có đủ khả năng lao động để tự lập nghiệp và góp phần xây dựng quê hương , đất nước , bảo vệ Tổ quốc Xã Hội Chủ Nghĩa
Chúc Bạn Thi Thật Tốt
Giúp mình câu này với ! với giải thichs giúp mình nhe!^^
TD
3 tháng 8 2021
( hot/ off/ Take/ it's/ hat/ your/ . )
=> Take off your hat it's hot.
Hc tốt
28 tháng 12 2021
\(\dfrac{x+y+2}{z}=\dfrac{y+z+3}{x}=\dfrac{z+x-5}{y}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2=\dfrac{2}{x+y+z}\\ \Rightarrow\left\{{}\begin{matrix}x+y+2=2z\\y+z+3=2x\\z+x-5=2y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y=2z-2\\y+z=2x-3\\z+x=2y+5\end{matrix}\right.\left(1\right)\)
Mà \(\dfrac{2}{x+y+z}=2\Rightarrow x+y+z=1\Rightarrow\left\{{}\begin{matrix}x+y=1-z\\y+z=1-x\\x+z=1-y\end{matrix}\right.\)
Thay vào hệ \(\left(1\right)\Rightarrow\left\{{}\begin{matrix}2z-2=1-z\\2x-3=1-x\\2y+5=1-y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3z=3\\3x=4\\3y=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=-\dfrac{4}{3}\\z=1\end{matrix}\right.\Rightarrow\left(x;y;z\right)=\left(\dfrac{4}{3};-\dfrac{4}{3};1\right)\)
Chọn A