Cho hình vuông ABCD ,M thuộc CD,N thuộc BC sao cho \(\widehat{BAN}=\widehat{NAM}\) .Chứng minh AM=MD+NB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
a) Vì ABCD là hình bình hành nên AB // CD.
Tứ giác AMCN có AM // CN (vì AB // CD); AM = CN (giả thiết).
Suy ra, tứ giác AMCN là hình bình hành.
Do đó AN = CM (đpcm).
b) Vì tứ giác AMCN là hình bình hành suy ra \(\widehat {AMC} = \widehat {ANC}\) (đpcm).
14 tháng 4 2022
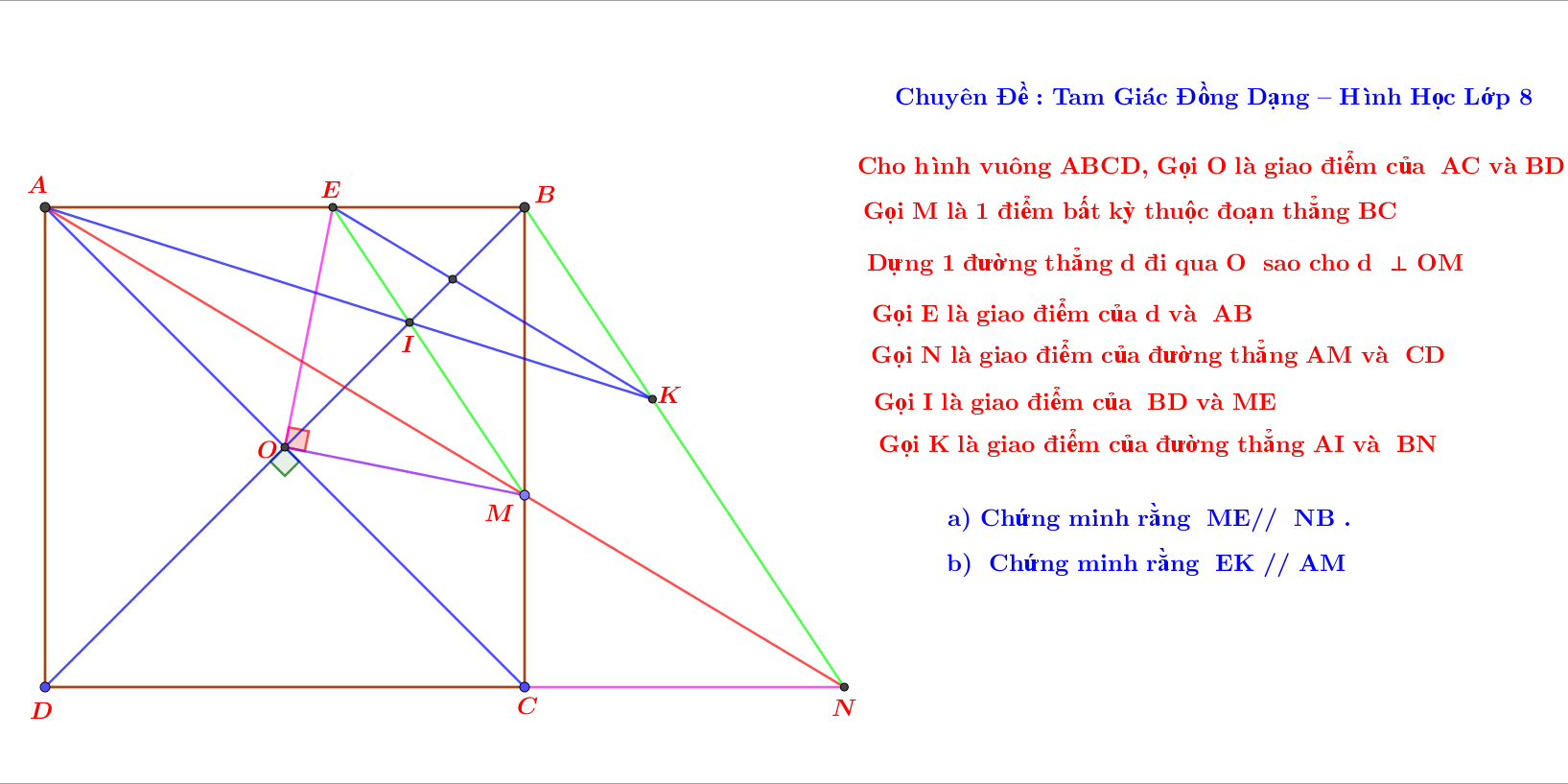
a. \(\widehat{AOE}=90^0-\widehat{BOE}=\widehat{BOM}\)
\(\Rightarrow\)△AOE=△BOM (g-c-g). \(\Rightarrow AE=BM;BE=CM\).
△MCN có: CN//AB \(\Rightarrow\dfrac{MN}{AM}=\dfrac{CM}{BM}=\dfrac{BE}{AE}\Rightarrow\)ME//NB.
8 tháng 2 2021
a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)