Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN

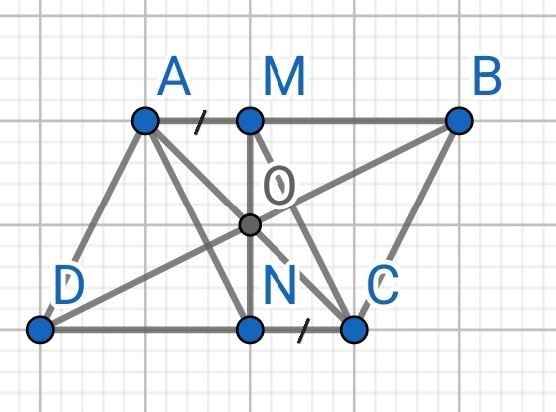 a) Do ABCD là hình bình hành
a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN

a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
b: AM+MB=AB
CN+ND=CD
mà MB=ND và AB=CD
nên AM=CN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
c: AMCN là hình bình hành
=>AN//CM
=>NK//MH
BMDN là hình bình hành
=>BN//DM
=>NH//KM
Xét tứ giác MKNH có
MK//NH
MH//NK
Do đó: MKNH là hình bình hành

a: Sửa đề; AMCN
Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
b:
Sửa đề: O là trung điểm của AC
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
c: Xét ΔOAI và ΔOCK có
góc OAI=góc OCK
OA=OC
góc AOI=góc COK
=>ΔOAI=ΔOCK
=>OI=OK
Xét tứ giác IMKN có
O là trung điểm chung của IK và MN
=>IMKN là hình bình hành
=>IM//NK

( bạn tự vẽ hình nha )
a, Vì M nằm tren cạnh AB, N nằm trêm cạnh CD => AM \(//\) CN
Mà AM=CN ( Theo gt) . Do đó tứ giác AMCN là hình bình hành ( Theo đk 3)
b, Vì ABCD là hình bình hành => Góc A= Góc C
Xét 2 tam giác AMP và tam giác CNQ bằng nhau theo TH c-g-c ( Tự CM )
=> MP=NC( 2 cạnh tương ứng )(1)
CMTT 2 tam giác MBQ và NDP ta được MQ=PN (2)
Từ (1) và (2) ta có MPNQ là hình bình hành (đpcm)
a) Vì ABCD là hình bình hành nên AB // CD.
Tứ giác AMCN có AM // CN (vì AB // CD); AM = CN (giả thiết).
Suy ra, tứ giác AMCN là hình bình hành.
Do đó AN = CM (đpcm).
b) Vì tứ giác AMCN là hình bình hành suy ra \(\widehat {AMC} = \widehat {ANC}\) (đpcm).