Chứng minh nếu [x;y] =1 và x.y là số chính phương thì x và y là số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 7 2016
Chứng minh bằng phản chứng :
Giả sử ngược lại, phương trình \(x^2=2\) có nghiệm \(x\in Q\) , tức là \(x=\frac{p}{q}\) (p,q \(\in Z,q\ne0\)) , \(\frac{p}{q}\) tối giản
Giải \(x^2=2\) được : \(x=\pm\sqrt{2}\)
Do đó: \(\sqrt{2}=\frac{p}{q}\) (Ta chỉ xét trường hợp \(x=\sqrt{2}\) , trường hợp \(x=-\sqrt{2}\) cũng tương tự)
Ta cần chứng minh \(\sqrt{2}\) không là số hữu tỉ.
Ta có : \(\sqrt{2}=\frac{p}{q}\Leftrightarrow p^2=2q^2\left(1\right)\Rightarrow p^2⋮2\Rightarrow p⋮2\) ( vì 2 là số nguyên tố)
Đặt \(p=2k\left(k\in Z\right)\Rightarrow p^2=4k^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow4k^2=2q^2\) nên \(q^2=2k^2\) (3)
Từ (3) lại có \(q^2⋮2\Rightarrow q⋮2\)
p và q cùng chia hết cho 2 nên phân số \(\frac{p}{q}\) không tối giản, trái với giả thiết.
Vậy \(\sqrt{2}\) không là số hữu tỉ, tức là \(x\notin Q\)
PT
1
KC
8 tháng 11 2021
mik cũng nghĩ vậy nên đăng lên đây hỏi ............ bạn xem sửa lại đề rồi làm lại giúp mik với
CM
29 tháng 6 2017
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
ND
0
27 tháng 1 2021
Ta có: \(x+4y=1\)
nên x=1-4y
Ta có: \(x^2+4y^2\ge\dfrac{1}{5}\)
\(\Leftrightarrow\left(1-4y\right)^2+4y^2-\dfrac{1}{5}\ge0\)
\(\Leftrightarrow16y^2-8y+1+4y^2-\dfrac{1}{5}\ge0\)
\(\Leftrightarrow20y^2-8y+\dfrac{4}{5}\ge0\)
\(\Leftrightarrow5\left(2y-\dfrac{8}{20}\right)^2\ge0\)(luôn đúng)
27 tháng 1 2021
Trả lời hộ mình nha máy mình lag k ấn được bình phương sorry các bạn nhé
CM
8 tháng 4 2019
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
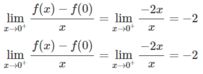
Mặt khác, với x < 0 thì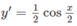 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
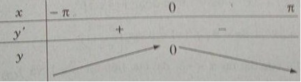
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
19 tháng 11 2021
\(\dfrac{x+2}{x-2}=\dfrac{y+3}{y-3}\Rightarrow\left(x+2\right)\left(y-3\right)=\left(x-2\right)\left(y+3\right)\\ \Rightarrow xy-3x+2y-6=xy+3x-2y-6\\ \Rightarrow6x=4y\\ \Rightarrow3x=2y\\ \Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\)