cho hình thang ABCD (AB//CD) trong đó hai đường phân giác của góc A và B cắt nhau tại điểm k thuộc đáy CD,Chứng minh rằng tổng hai cạnh bên bằng đáy CD của hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BL
18 tháng 6 2017
Ta có Ab song song với Dc=> BAK=AKD
mà BAK=DAK( do Ak là tpg của DAB)
=> DAk=AKD=> tam giác DAk cân tại D=>DA=Dk(1)
chứng minh tương tự với tam giác BKC => tam giác BkC cân tại BKC cân tại C=> BC=KC(2)
Cộng (1),(2) => DA+BC=DK+KC
=> Da+Bc=DC
6 tháng 8 2018
Lời nói chẳng mất tiền mua. Lựa lời mà chửi cho vừa lòng nhau. Đã chửi, phải chửi thật đau. Chửi mà hiền quá còn lâu nó chừa. Chửi đúng , không được chửi bừa . Chửi cha mẹ nó , không thừa một ai . Khi chửi , chửi lớn mới oai. Chửi hay là phải chửi dài , chửi lâu . Chửi đi chửi lại mới ngầu. Chửi nhiều cho nó nhức đầu , đau tai. Chửi xong nhớ nói bái bai . Phóng nhanh kẻo bị ăn chai vào mồm.
21 tháng 6 2019
Câu hỏi của Thư Anh Nguyễn - Toán lớp 8 - Học toán với OnlineMath. Em tham khảo link này nhé!
CM
3 tháng 12 2017
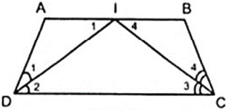
Áp dụng tính chất so le của AB//CD và giả thiết ta có:
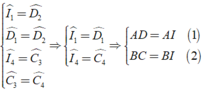
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)
Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB
Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
a) Theo đề bài ta có: \(\widehat{DAF}+\widehat{ADF}=\frac{\widehat{DAB}+ADC}{2}=\frac{180^o}{2}=90^o\)
Xét tam giác AFD có \(\widehat{DAF}+\widehat{ADF}=90^o\) nên \(\widehat{AFD}=90^o\)
Hay tam giác AFD vuông tại F.
Gọi E là trung điểm AD.
Xét tam giác vuông ADF có FE là trung tuyến ứng với cạnh huyền nên EF = AD/2
Lại có do F là trung điểm BC; E là trung điểm AD nên EF là đường trung bình hình thang.
Từ đó suy ra \(EF=\frac{AB+BC}{2}\)
Vậy nên AD = AB + BC.
b) Giả sử AD = AE + ED.
Gọi E là trung điểm AD. Do AD = AB + CD nên FE = (AB + DC)/2
Ta có E là trung điểm AD. Vậy nên EF là đường trung bình hình thang hay hay Flà trung điểm BC.
15 tháng 9 2019
Tham khảo : Câu hỏi của Trần Nhật Duy - Toán lớp 8 - Học toán với OnlineMath
nếu hình hơi bé bạn vào link này : https://hoc24.vn/images/discuss/1632366020_614bedc45d934.jpg